Понятие системы связи, сети связи, страница 48

Наличие хотя бы одного ненулевого элемента в комбинации синдрома свидетельствует о наличии в принятой комбинации ошибок.

Пример:

Пусть передавалась комбинация (0001001) линейного (7,4)-кода, задаваемого первым набором коэффициентов (C_ji), а была принята комбинация (0101001).

Найдем синдром принятой комбинации:

Сумму (6) иногда называют проверкой на четность. Основанием к тому послужило то, что как видно из правил формирования проверочных символов: проверочный символ = 1, если число 1 в соответствующих информационных символах нечетно и раен 0, если число 1 в этих символах четно. Поэтому, если комбинация линейного кода принята без искажений, то для нее всегда справедливо: в каждой группе символов, по которой находится элемент синдрома 1 четно.

Обнаружение ошибок в комбинациях линейных кодов при использовании для их описания ТМ основано на применении проверочной матрицы H. К этой матрице можно прийти из следующих рассуждений: каждый символ s_j в формуле (6) можно рассматривать как скалярное произведение с операцией сложения по mod2 двух r-элементных последовательностей.

Одна из которых является принятой V^*, а вторая состоит из коэффициентов C_ji на первых k позициях и 1 с (r-1) нулем на последних r позициях. Причем 1 занимает (k + j)-тую позицию. Таким образом формулу (6) будем рассматривать так:

У кода с r проверочными символами r последовательностей  Если все их записать в прямоугольнукю таблицу, то получим матрицу размера , называемую проверочной матрицей Н линейного кода:

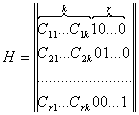 r строк            (7)

Матрица Н имеет следующую структуру: первые k ее столбцов представляют собой транспонированную матрицу коэффициентов , входящую в порождающую матрицу G.