Понятие системы связи, сети связи, страница 58

Первая из этих последовательностей - коэффициенты многочлена A(X), а вторая – сдвинутый циклически на (n-1)-i вправо комбинации  многочлена , получаемый из B(X) в результате записи его степеней в обратном порядке.

В многочлене (4) произведение вида  появились в результате применения равенства .

Очевидно, что если многочлены A(X) и B(X) ортогональны, то все коэффициенты C_i, для i = 0,1,...,n-1, равны нулю.

Учитывая формулу (3) можно утверждать, что скалярное произведение любой комбинации циклического кода и любой из n возможных последовательностей, получаемых в результате циклического сдвига вправо последовательности, соответствующей многочлену равны нулю. Указанные n последовательностей легко получить по многочлену , умножая его на .

Поскольку многочлен имеет степень k, то первые r последовательностей, соответствующие многочленам  за счет разных степеней последних линейно независимы.

Образуем матрицу Н_ц размером , в качестве строк которой возьмем r указанных линейно независимых последовательностей, т.е. образуем матрицу:

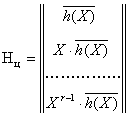
Каждую из этих последовательностей дополним справа r-1 нулем до длины n. Эта матрица обладает тем свойством, что для любой комбинации V с порождающим многочленом g(X)

    (5)

С другой стороны, выполнение равенства (3) для какой-либо комбинации длины n свидетельствует о ее принадлежности циклическому коду. В силу этого матрица Н_ц называется проверочной матрицей циклического кода, а многочлен h(X), на основе которого она строится проверочным многочленом этого кода. Нетрудно видеть, что матрица Н_ц и матрица Н линейного кода различаются по своей структуре. Однако в результате применения элементарных операций над строками матрицу Н_ц можно  привести к матрице Н. Полученная в этом случае матрица Н также будет обладать свойством: