Другими словами, код называется линейным, если при (j=1,..r)
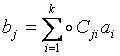 (1)
(1)
Выбор линейных функций (1) для некоторого кода полностью задает закон его построения. В свою очередь, как видно из (1), каждая из зависимостей (каждая линейная сумма) задается при помощи k коэффициентов Сji, следовательно, все линейные суммы задаются при помощи kr коэффициентов Сji.
Пример:
Построить линейный (7, 4) – код, задаваемый следующим набором k*r = 3*4 = 12 коэффициентов Сji.
|
С11=1 |
С12=1 |
С13=0 |
С14=0 |
|
С21=0 |
С22=1 |
С23=1 |
С24=0 |
|
С31=0 |
С32=0 |
С33=1 |
С34=1 |
Запишем правило формирования проверочных символов для этого кода:
![]() ,
,
![]() ,
,
![]()
Строим все 24 = 16 комбинаций этого линейного кода. Построение выполним в таблице.
|
№ комбинации |
a1 a2 a3 a4 b1 b2 b3 |
Вес комбинации |
|
1 |
0 0 0 0 0 0 0 |
0 |
|
2 |
0 0 0 1 0 0 1 |
2 |
|
3 |
0 0 1 0 0 1 1 |
3 |
|
4 |
0 0 1 1 0 1 0 |
3 |
|
5 |
0 1 0 0 1 1 0 |
3 |
|
и так далее |
||
|
16 |
1 1 1 1 0 0 0 |
4 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.