Понятие системы связи, сети связи, страница 26

здесь V­_ki ,V­­­_kj  - k-тые координаты точек i,j.

Расстояние между двумя точками, удовлетворяющее следующим 3 условиям:

·    x=y

· 

· 

называется метрикой.

Соединим каждую точку рассматриваемого пространства прямыми линиями со всеми точками, удаленными на расстояние . Полученную геометрическую фигуру, имеющую сеточную структуру, называют геометрической моделью n-разрядного m-ичного кода. Точки дискретного пространства, которые содержит указанная геометрическая фигура называются вершинами, а соединяющие их отрезки – ребрами.

Примеры:

• Построить геометрическую модель двоичного двухразрядного кода.

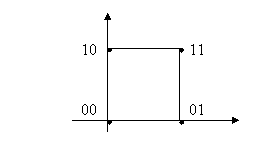
·  Построить геометрическую модель двоичного трехразрядного кода.

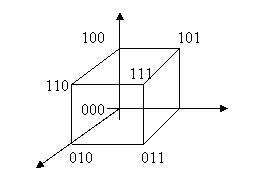
Геометрическая фигура, являющаяся моделью двоичного n-разрядного кода, получила название n-мерного куба.

Расстояние между любыми двумя вершинами такого куба, т.е. между двумя кодовыми комбинациями, можно трактовать из формулы (1) как число разрядов, в которых отличаются эти комбинации. Так, например, расстояние между комбинациями 011 и 110 равно 2, т.к. эти комбинации отличаются значениями двух символов в первом и третьем разрядах. Отличие символов в одноименных разрядах комбинаций различного кода легко выясняется в результате применения к ним операции сложения по модулю два. Результат сложения только тогда равен единице, когда складываемые числа различаются. Учитывая это расстояние между двумя комбинациями n-разрядного двоичного кода можно определить так:

    (2)

\

Обозначим через V_l комбинацию, представляющую собой сумму по модулю два комбинаций V_i  и V_j, то есть .