Понятие системы связи, сети связи, страница 25

Этот способ представления применим только для достаточно коротких равномерных кодов.

Задание кода в виде кодового дерева

При этом способе каждая комбинация представляется вершиной кодового дерева.

Кодовое дерево – граф, состоящий из точек и расходящихся из них линий, заканчивающихся так же точками.

Точки графа – вершины, а соединяющие их отрезки прямых – ребра. Начальная вершина, от которой начинается расхождение ребер – корень дерева. Число ребер, которое надо пройти от корня дерева к некоторой вершине – порядок вершины. Максимальное число ребер, которое может выходить из некоторой вершины, равно основанию кода, а максимальный порядок вершин равен максимальной длине комбинаций кода.

Символы комбинации, приписываемой каждой вершине, определяются направлением движения по ребрам от корня дерева к данной вершине. Движение от корня к вершинам первого порядка определяет значение первого слева символа комбинации. Направление движения от вершины первого порядка к вершине второго порядка определяет значение второго слева символа комбинации и так далее.

Пример:

Построить кодовое дерево двоичного трехразрядного кода.

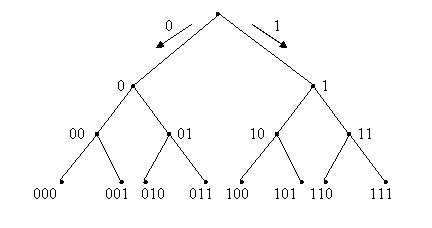
Данный способ применим для представления как равномерных, так и неравномерных кодов.

Геометрическая модель кода

Этот способ состоит в изображении комбинаций кода точками n-мерного дискретного векторного пространства.

Пусть имеем блоковый равномерный n-разрядный m-ичный код. Каждую комбинацию такого кода V = (V_n ,…, V₂ ,V₁) можно рассматривать как вектор или точку некоторого n- мерного векторного пространства с координатамиV₁ ,V₂,…, V_n .

Вектор – упорядоченная последовательность чисел.

Если m конечно и любая координата вектора представляет собой целое положительное число от 0 до (m-1), то указанный код можно рассматривать как n-мерное дискретное пространство, состоящее из N = mⁿ   точек, соответствующих концам всех  mⁿ  векторов.

Условимся, что число V_k – это координата точки пространства по k-той оси. В математике для каждого пространства вводится понятие расстояние между двумя точками V­_i ,V­­­_j (i,j = 1,2,…N) определяется так:     (1)