Понятие системы связи, сети связи, страница 57

35. Проверочный многочлен и проверочная матрица циклического кода

Рассмотрим многочлен h(X) степени k, представляющий собой частное от деления двучлена Xⁿ + 1 на g(X), т.е. рассмотрим многочлен:

            (1)

Этот многочлен имеет вид:  

Этот многочлен играет такую же большую роль в теории циклических кодов как и g(X). Эта роль объясняется одним интересным свойством.

Пусть  

    (2)

многочлен, представляющий любую комбинацию циклического кода с порождающим многочленом g(X).

Выразим g(X) из формулы (1) и подставим в формулу (2), получим:

Приведем к общему знаменателю:

Заменим:

Получим:

        (3)

Свойство многочлена h(X):

Многочлен h(X) ортогонален любому многочлену V(X), представляющему комбинацию циклического кода.

Два многочлена называются ортогональными, если их произведение равно нулю.

Пусть имеем два многочлена степени n-1:

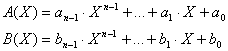
Найдем многочлен C(X), являющийся их произведением, и запишем его с учетом равенства .

C(X) имеет вид:

   (4)

Коэффициент при степени , где i = 0,1,..,n-1, в многочлене C(X) равен:

Нетрудно видеть, что C_i является скалярным произведением с операцией сложения по модулю два двух n-элементных последовательностей, записываемых: