Понятие системы связи, сети связи, страница 36

Для того, чтобы код мог обнаруживать любую одиночную ошибку в любой своей комбинации необходимо, чтобы при таких ошибках разрешенная комбинация переходила в запрещенную.

Это возможно только тогда, когда d>1 или учитывая, что d – целое, d ≥ 2.

Пример:

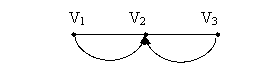
d(V₁, V₂) = 2

d(V₁, V₃) = 1

d(V₂, V₃) = 1

Если d ≠ 2, то найдется такая пара, в которой разрешенная комбинация перейдет в запрещенную.

Для того, чтобы код позволял обнаруживать ошибки кратности ν₀ и менее, необходимо, чтобы его d удовлетворяло условию:

     (1)

Пусть ν₀ = 3 → d ≥ 4

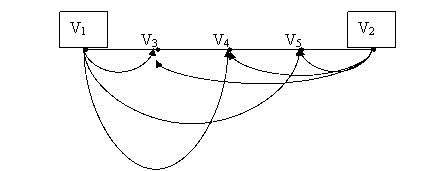
Несколько сложнее обстоит дело с исправлением ошибок. Обычно при исправлении ошибок преследуют цель минимизировать вероятность выдачи ложной кодовой комбинации получателю. Естественно, что достижение этой цели возможно только при учете статистики появления ошибок в канале. Зная такую статистику, нетрудно выполнить разбиение множества запрещенных комбинаций U на подмножества А_i так, что вероятность неправильного исправления ошибок была минимальна.Статистика ошибок в комбинациях кода определяется каналом. Для всех используемых на практике каналов такая статистика получена. Это позволило разработать различные математические модели с той или иной степенью точности, представляющие процесс передачи двоичных символов комбинаций по каналу. В настоящее время известно более 25 различных математических моделей каналов. Из всех моделей мы рассмотрим только одну: двоичный симметричный канал без памяти. В отношении этой модели корректирующие коды исследованы наиболее полно. Ориентация на двоичный симметричный канал без памяти объясняется простотой этой модели, несмотря на то, что она лишь весьма приближенно представляет процесс передачи символов по реальным каналам.

Действительно искажения символов комбинаций кода при передаче по такому каналу считаются независимыми событиями. Вероятность искажения нуля равна вероятности искажения единицы, т.е. p₀ = p₁ = p, где p – вероятность искажения двоичного символа.