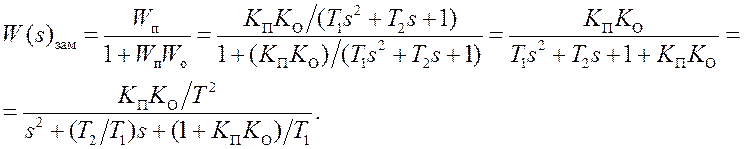
Согласно критерию Гурвица для устойчивости такой системы нужно, чтобы:
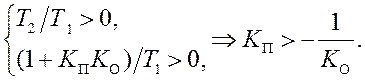
Так как на практике объектов с отрицательными постоянными времени не существует, система устойчива всегда.
4) Система со звеном третьего порядка в качестве объекта, ООС и П-регулятором устойчива не всегда:
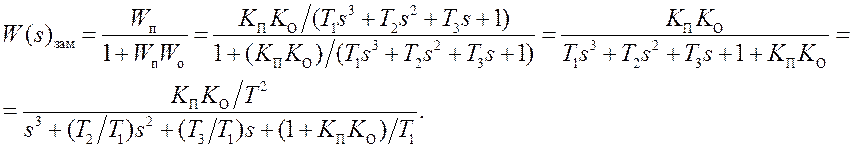
Согласно критерию Гурвица для устойчивости такой системы нужно, чтобы:
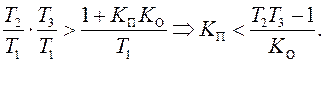
Явно представлена зависимость устойчивости такой системы от параметров объекта.
Очевидно, что устойчивость систем большего порядка так же зависит от параметров самого объекта.
Кроме того, система с любым объектом, степень знаменателя которого на лишь на единицу выше степени числителя – устойчива!
Если решение расходится, то прежде всего надо попытаться уменьшить временной шаг интегрирования. Однако это неизбежно приводит к увеличению числа шагов моделирования и увеличению его общего времени. Поэтому в моделях, результаты моделирования которых представляются кривыми с разными (медленными и быстрыми) участками, полезно применение адаптивных методов интегрирования, допускающих автоматическое изменение шага интегрирования. К таким методам относятся адаптивный метод Рунге—Кутта 5-ого порядка и адаптивный метод Булирша—Стоера. Для них можно определить минимальный размер шага.
Если объект устойчив, то введением П регулятора систему можно сделать неустойчивой, а если не устойчив, то введение П регулятора устойчивым его не сделает.
1) Моделирование известных структур.
Существует класс задач, где необходимы предварительные испытания моделей, необходимо также и тестирование тестов, т.е. апробация моделей. Испытание моделей должно осуществляться на задачах, решение которых известно и без применения моделей. Решение неизвестных задач должно осуществляться методами моделирования, успешно испытанными ранее. Никогда не должно быть при решении задачи более одной неопределенности: либо неизвестна задача, либо неизвестен метод. Если задача новая и метод новый, то результаты будут недостоверными.
2) Изменение шага интегрирования.
Шаг интегрирования имеет очень большое значение, но проверка корректности выбора шага интегрирования очень проста – изменение шага интегрирования в небольших пределах не должно менять вида переходного процесса. Проверка корректности осуществляется дополнительным уменьшением шага интегрирования. Если при уменьшении шага, переходный процесс не меняется, это косвенно свидетельствует о том, что шаг интегрирования выбран корректно. Если же меняется (а тем более – принципиально меняется), то шаг интегрирования слишком велик, и его следует уменьшить.
3) Изменение параметров в небольших пределах.
Изменение параметров системы в небольших пределах при условии, что система не находится вблизи границы устойчивости, меняет переходные процессы незначительно, не качественно, а количественно.
4) Показательные примеры с нереализуемыми звеньями.
Также новое программное обеспечение нужно проверять на простом и провокационном примерах. Простой пример должен сработать, а провокационный пример должен работать правильно. Например, для проверки можно включить звено запаздывания e-TS, на переходном процессе будут представлены колебания, затем в регулятор включить звено предугадывания e+TS. Если система получится более устойчивой, то программный продукт работает неправильно – т.к. невозможно сделать звено предугадывания.
Количество тестов определяет разработчик системы. Они должны быть достаточными, чтобы снять все сомнения в правильности моделирования.
Принцип симуляции (Simulation) – каждый элемент формирует отклик на входные воздействия в зависимости от своей модели и от своего состояния.
Шаг интегрирования – малый интервал времени, на котором рассчитывается отклик. Он должен быть настолько мал, чтобы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.