Основные особенности и возможности программы VisSim. Режимы работы. Структурная устойчивость или неустойчивость некоторых простейших замкнутых линейных систем, упрощенный критерий устойчивости по ЛАЧХ, условие его применимости, связь этого условия с шагом интегрирования при моделировании. Параллельное включение двух звеньев – свойства результирующего звена, свойства а.ч.х. и ЛАЧХ. Разделение движений по двум каналам управления. Разделение движений по двум датчикам с различными шумовыми свойствами в различн, страница 31

Любой замкнутый контур, передаточная функция которого в разомкнутом виде описывается рациональной дробью, степень знаменателя которой лишь на единицу больше степени числителя (что имеет место для объектов первого порядка), не имеет смысла аналитически оптимизировать, моделировать или рассчитывать каким-либо программным обеспечением. Поскольку условия нарушения устойчивости при моделировании никогда не будут выполнены, либо будут выполнены при параметрах, не имеющих никакого отношения к реальному объекту.

А)нет, поскольку объект первого порядка с пропорциональным регулятором всегда устойчив.

Б)да, поскольку нет объектов первого порядка.

В)да, поскольку при моделировании может быть неверно задан шаг интегрирования.

Г)при некорректном – да, при корректном – нет.

52.Может ли объект второго порядка быть доведен до неустойчивого переходного процесса с пропорциональным регулятором: а) теоретически; б) на практике; в) при моделировании как таковом; г) при моделировании в VisSim (корректном или не корректном)?

Рассмотрим простейший случай, когда в качестве регулятора используется коэффициент усиления:

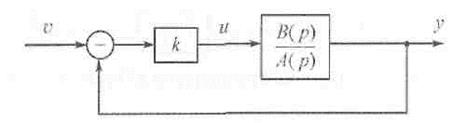
Т.к. звено второго порядка, то В(р)=b, A(p)=p²+a₂p+a₁

Характеристический полином замкнутой системы: p²+a₂p+a₁+kb

Рассмотрим характеристический полином замкнутой системы в области высоких частот ≈p²+kb=0 (рассматриваем только старшие степени при р в А(р) и В(р))

Таким образом, имеем пару мнимых корней , т.е. система находится на границе устойчивости (в теории). На практике же, с увеличением k система теряет устойчивость? т.к. она «раскачивается» на быстрых движениях.

При моделировании устойчивость при увеличении k зависит от шага интегрирования, чем он меньше, тем при больших значениях k система еще устойчива, но все же, при некотором значении k, она становится неустойчивой (как в VisSim, так и в Matlab)

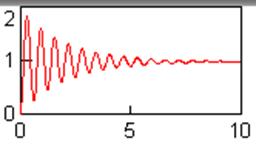увеличили k, шаг интегриров. не меняли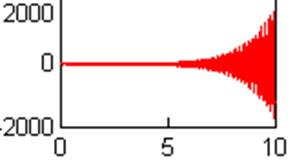

При  увеличении коэффициента быстродействие системы возрастает, поэтому после некоторого достигнутого быстродействия шаг интегрирования становится уже не достаточно мелким. Это породит нарушение устойчивости системы при дальнейшем увеличении коэффициентов.

А)нет, может быть только на границе устойчивости.

Б)да

В)да, поскольку при моделировании может быть неверно задан шаг интегрирования.

Г)при некорректном – да, при корректном – нет.

53.Имеет ли смысл понятие «оптимальная настройка» для системы из объекта первого, второго, третьего и четвертого порядка с ПИД-регулятором (по каждому случаю отвечать отдельно): а) теоретически; б) на практике; в) при моделировании как таковом; г) при моделировании в VisSim (корректном или не корректном)?

Вообще говоря, поиск «оптимальной настройки» ПИД-регулятора для системы, представленной уравнением первого и второго порядков – задача не корректная, в смысле отсутствия экстремума любого стоимостного функционала от настраиваемых параметров, т.е. оптимальной настройки не существует.

При любой настройке можно указать другое значение коэффициентов, новое, при котором и переходный процесс будет быстрее, и перерегулирование не более и тд. Для объекта второго порядка имеет смысл понятие оптимальный ПИ – регулятор.

При моделировании оптимальная настройка может существовать при конкретных параметрах моделирования, например, конкретном шаге интегрирования.

На практике же для любого без исключения объекта всегда существует наилучшая настройка. Это связано с тем, что не существует идеальных объектов ни первого, ни какого-либо конечного порядка в неограниченном диапазоне частот и без учета ограничений входного воздействия. Именно эти ограничения приводят к оптимальности на практике определенных параметров регулятора. Существование оптимального решения вызвано ограниченностью достижимого быстродействия и качества переходного процесса.

При корректном моделировании система с ПИД-регулятором устойчивость системы не нарушается, а быстродействие может повышаться при соответствующем увеличении коэффициентов регулятора, что согласуется с теорией.