Основные особенности и возможности программы VisSim. Режимы работы. Структурная устойчивость или неустойчивость некоторых простейших замкнутых линейных систем, упрощенный критерий устойчивости по ЛАЧХ, условие его применимости, связь этого условия с шагом интегрирования при моделировании. Параллельное включение двух звеньев – свойства результирующего звена, свойства а.ч.х. и ЛАЧХ. Разделение движений по двум каналам управления. Разделение движений по двум датчикам с различными шумовыми свойствами в различн, страница 22

Если система нелинейная, то нельзя говорить о реакции на ступеньку. Можно говорить о реакции на те виды воздействия, которые реально присутствуют. Нужно иметь правильную модель, принять во внимание все значения, смещения, ограничения, шумы. Единственное, можно вводить масштаб времени, чтобы не иметь слишком больших или маленьких коэффициентов. Он должен быть единым для модели и регулятора. Упрощать или пренебрегать чем-то в случае нелинейных систем нельзя.

35.Критерии оптимальности настройки при моделировании. Их назначение, суть, способы применения, отличия, необходимые свойства.

Под постановкой задачи оптимизации будем понимать следующие условия:

1) обоснованность математической модели  объекта - задание ее с такой степенью подробности, при которой теоретически оптимальный регулятор совпадает с практически оптимальным;

2) обоснованность целевых функционалов – такое их формулирование, при которых достижение их минимума гарантирует наилучшее соответствие свойств замкнутой системы предъявляемым к ней техническим требованиям.

J% - перерегулирование

P(e) – энергия (интеграл от мощности) ошибки

Q, L, N, M, R1, R2, R3 – целевые функции, определенные интегральными соотношениями от ошибки, её производной и (или) квадратичной формы или абсолютной величины, а также можно ввести умножение на время t с начала переходного процесса.

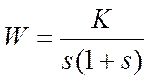Модель для отыскания оптимального коэф усиления при заданной пост, времени

Все те целевые функции, кроме N(e), имеют экстремум вблизи параметра, соответствующего устойчивому переходному процессу, пригодны для роли критерия оптимальности настройки ПИД-регулятора (в зависимости от целей настройки).

Целевые функции, не имеющие экстремума, но монотонно изменяющиеся, могут быть использованы для создания сложной целевой функции, в которую они будут входить в качестве слагаемого с весовым коэффициентом.

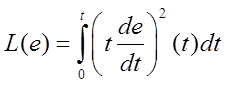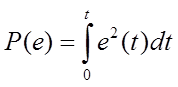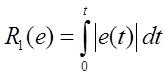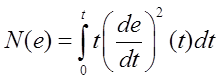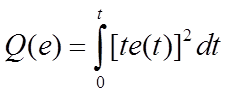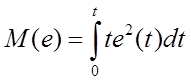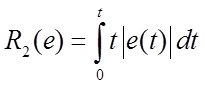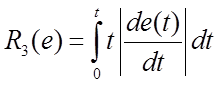Критерии монотонности переходного процесса, Любой из этих  критериев пригоден для выявления колебательности переходного процесса (перерегулирования)

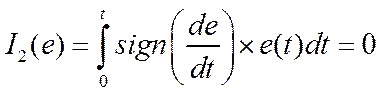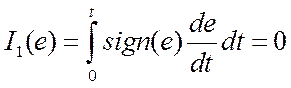Любой из этих критериев пригоден для выявления колебательности переходного процесса (перерегулирования)

36.Влияние метода интегрирования при цифровом управлении на результаты; способ выявления этого влияния моделированием в программе VisSim, перенос результатов на свойства реальных цифровых интеграторов и дифференцирующих устройств. Какой метод интегрирования предпочтителен при моделировании замкнутых САУ?

При моделировании имеется возможность выбора метода интегрирования, единого для всей моделируемой схемы. Варианты методов составляют: Эйлера, трапеций, Рунге-Кутта 2 порядка, Рунге-Кутта 4 порядка, адаптивный Рунге-Кутта 5 порядка, адаптивный Булериш-Стойера и Эйлера с упреждением.             Выбор метода оказывает влияние не только на точность и корректность операции интегрирования, но и на результаты дифференцирования, которое вычисляется через интегрирование.

(проводилось моделирование этой модели)

При моделировании интегрирования производных:

·  По методу трапеций и Булериш-Стойера сигнал при прохождении через блок дифференцирования и интегрировании оказывается равным нулю. 

·  Рунге-кута  2 порядка и 5 порядка– форма  сигнала при прохождении через те же блоки примерно соответствовала  форме исходного но максимальное значение амплитуды сигнала и значения сигнала в уст. режиме меньше фактически на 2 порядка.

·  Рунге-кута  4 порядка– тоже самое только сигнал на порядок меньше

Только простой метод Эйлера (без упреждения) позволяет корректно моделировать в данном пакете все динамические системы, не зависимо от порядка следования линейных звеньев.