Основные особенности и возможности программы VisSim. Режимы работы. Структурная устойчивость или неустойчивость некоторых простейших замкнутых линейных систем, упрощенный критерий устойчивости по ЛАЧХ, условие его применимости, связь этого условия с шагом интегрирования при моделировании. Параллельное включение двух звеньев – свойства результирующего звена, свойства а.ч.х. и ЛАЧХ. Разделение движений по двум каналам управления. Разделение движений по двум датчикам с различными шумовыми свойствами в различн, страница 8

Под точностью системы понимается величина, обратно пропорциональная относительной погрешности. Если у системы погрешность 0,5%, то точность системы 200. Эту величину применяют редко в силу того, что она создает путаницу в терминологии.

Статическая погрешность – термин из метрологии. Она существует всегда у любой системы измерения. Никогда не равно 0.

Суммирование погрешностей – возвести в квадрат, сложить и извлечь корень.

10.Структурная устойчивость или неустойчивость некоторых простейших замкнутых линейных систем, упрощенный критерий устойчивости по ЛАЧХ, условие его применимости, связь этого условия с шагом интегрирования при моделировании.

Пример структурно устойчивой системы – система первого порядка с пропорциональным регулятором устойчива при любых коэффициентах. Это не относится к случаю с ПОС.

Пример структурно неустойчивой системы – система второго порядка с большим коэффициентом усиления, два интегратора (идеальных) и обратная связь.

Критерий устойчивости по ЛАЧХ и ЛФЧХ (логарифмический критерий Найквиста).

Рисуем в одних осях ЛАЧХ и ЛФЧХ. Для того, чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы на всех частотах, где ЛАЧХ устойчивой разомкнутой системы положительна, ЛФЧХ не достигала значения –ПИ.

РИСУНОК

Упрощенный критерий Найквиста состоит в том, что если система минимально фазовая (фазовая характеристика определяется только линейными членами вида рациональной дроби, нет звена чистого запаздывания), тогда наклон жестко связан с ФЧХ и он должен быть 20 дБ/дек ± диапазон запаса. 40 – это уже граница устойчивости. Чем более протяженный этот участок, тем больше запас устойчивости.

11.Система с каким объектом всегда может быть сделана устойчивой введением И-регулятора (а с каким не всегда может)? То же применительно к моделированию с фиксированным и с изменяемым шагом интегрирования.

1)  Система с интегратором в качестве объекта, ООС и И-регулятором всегда находится  на границе устойчивости:

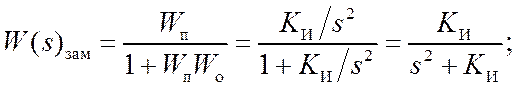
Система всегда находится на границе устойчивости, как бы мы не изменяли . Моделирование в VisSim подтвердило данные теоретические выводы.

2)  Система с апериодическим звеном в качестве объекта, ООС и И-регулятором всегда устойчива:

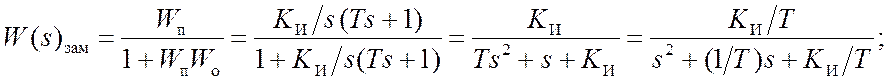
Согласно критерию Гурвица для устойчивости такой системы нужно, что бы:

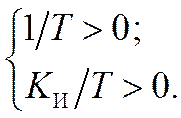
Так как на практике объектов с отрицательными постоянными времени не существует, то при положительном  система всегда будет устойчивой.

3)  Система с колебательным звеном в качестве объекта, ООС и И-регулятором устойчива не всегда:

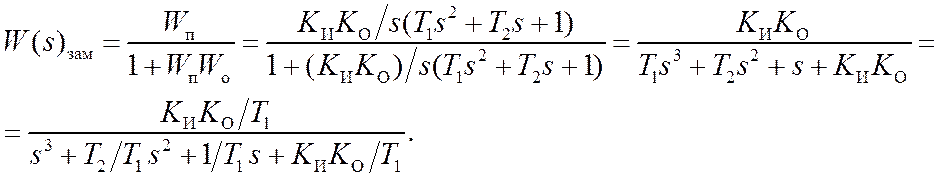
Согласно критерию Гурвица для устойчивости такой системы нужно, чтобы:

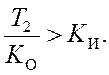
Явно представлена зависимость устойчивости такой системы от параметров объекта.

Очевидно, что устойчивость систем большего порядка так же зависит от параметров самого объекта.

Если решение расходится, то прежде всего надо попытаться уменьшить временной шаг интегрирования. Однако это неизбежно приводит к увеличению числа шагов моделирования и увеличению его общего времени. Поэтому в моделях, результаты моделирования которых представляются кривыми с разными (медленными и быстрыми) участками, полезно применение адаптивных методов интегрирования, допускающих автоматическое изменение шага интегрирования. К таким методам относятся адаптивный метод Рунге—Кутта 5-ого порядка и адаптивный метод Булирша—Стоера. Для них можно определить минимальный размер шага.

Если объект устойчив, то введением П регулятора систему можно сделать неустойчивой, а если не устойчив, то введение П регулятора устойчивым его не сделает.

12.Система с каким объектом всегда может быть сделана устойчивой введением П-регулятора (а с каким не всегда может)? То же применительно к моделированию с фиксированным и с изменяемым шагом интегрирования.

1)  Система с интегратором в качестве объекта, ООС и П-регулятором всегда устойчива:

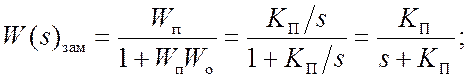
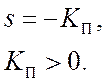
2)  Система с апериодическим звеном в качестве объекта, ООС и П-регулятором всегда устойчива:

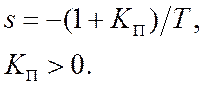
3)  Система с колебательным звеном в качестве объекта, ООС и П-регулятором устойчива всегда: