Основные особенности и возможности программы VisSim. Режимы работы. Структурная устойчивость или неустойчивость некоторых простейших замкнутых линейных систем, упрощенный критерий устойчивости по ЛАЧХ, условие его применимости, связь этого условия с шагом интегрирования при моделировании. Параллельное включение двух звеньев – свойства результирующего звена, свойства а.ч.х. и ЛАЧХ. Разделение движений по двум каналам управления. Разделение движений по двум датчикам с различными шумовыми свойствами в различн, страница 37

69.Как осуществить оптимизацию регулятора для объекта размерностью 2х2 в программе VisSim? Каковы при этом требования к тестовым сигналам, к критерию качества?

Для оптимизации объекта 2х2 (или другого многомерного объекта) используется целевая функция, выбранная в качестве критерия оптимизации. Выбор конкретного критерия зависит от поставленной задачи, например: если требуется очное поддержание текущей производительности, то следует выбирать критерий от модуля ошибки: чем быстрее ошибка сведется к нулю, тем выше будет достигнута текущая производительность. Если требуется поддержание точности за какое-то время или на какой-то объем продукции, то следует выбирать критерий точности от интеграла модуля ошибки. Для многомерных объектов критерием качества будет не просто ошибка, а сумма ошибок (или их модулей) от каждого канала.

Тестовые сигналы должны подаваться следующим образом: величина тестовых сигналов одинакова, один сигнал подается при начале моделирования, второй – через время, равное половине всего времени моделирования.

70.Локальные и глобальные минимумы, их влияние на результат оптимизации.

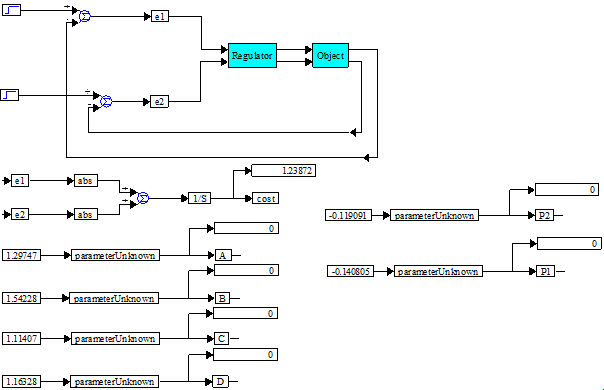
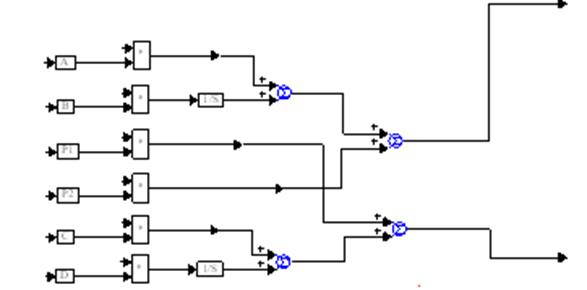
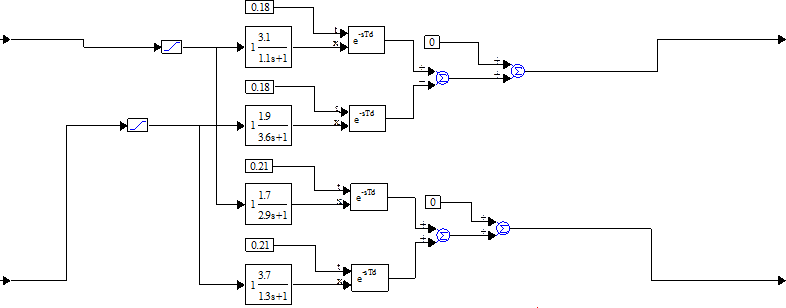
Оптимизация модели заключается в таком подборе ее параметров, при котором обеспечивается минимум некоторой целевой функции, например, определяющей значение каких-либо параметров. Оптимизация завершенной модели является целью многих задач моделирования. В VisSim она реализуется особым построением модели, в которую включаются специальные блоки для многократного моделирования с изменяемыми параметрами. Изменение параметров производится итерационно до получения минимума некоторой целевой функции системы. Задачей пользователя является подготовка модели таким образом, чтобы целевая функция обеспечивала достаточно хорошо выраженный минимум.

Нередко встроенным в VisSim оптимизаторам удается найти глобальный минимум целевой функции. Но, в общем случае многоэкстремальных целевых функций глобального минимума оптимизация найти не может. Решение может сойтись к локальному минимуму. Однако изменением параметров оптимизации можно найти имеющиеся минимумы (если их не слишком много) и затем определить, какой же из них является глобальным.

Установка общих параметров оптимизации можно выполнить из окна установок оптимизации,  которое выводится командой optimization Properties в позиции Simulations  меню.

Что касается оптимизации в других имитирующих программах, например, Simulink, который предоставляет в распоряжение пользователя графический интерфейс для настройки параметров динамических объектов, обеспечивающих требуемое качество переходных процессов. В качестве средства для достижения указанной цели принимается оптимизационный подход, обеспечивающий минимизацию функции штрафа за нарушение динамических ограничений

Следует отметить, что процесс выполнения оптимизации в Matlab не очевиден (в отличие от VisSim), поскольку не требует задания никакой целевой функции. Таким образом, результаты оптимизации, получены в ПО Matlab могут быть поставлены под сомнение.

71.Каким образом можно выявить немонотонность переходного процесса (не только и не столько перерегулирование), каким образом следует видоизменить критерий качества, чтобы это свойство подавлялось при оптимизации?

Передаточная функция объекта:

Определить немонотонность переходного процесса можно по параметрам объекта: немонотонность переходного процесса зависит от коэффициента демпфирования d. Если , то корни характеристического уравнения будут комплексно - сопряженными.Колебания будут тем больше, чем меньше  d.

ОГРАНИЧЕНИЕ КОЛЕБАТЕЛЬНОГО ВИДА ПЕРЕХОДНОГО ПРОЦЕССА

В данном случае речь идет о колебании переходного процесса по мере его развития. Признаком таких колебаний служит совпадение знака ошибки и ее производной. Такая ситуация должна быть признана, разумеется, нежелательной. Выявление этой ситуации достигается умножением ошибки на ее производную. Полученный результат должен быть отрицательным. Следует применить ограничитель этой величины снизу, настроенный на ноль, а с выхода ограничителя сигнал умножить на большой коэффициент и результат приплюсовать к модулю ошибки, используемой для вычисления стоимостного функционала.