Основные особенности и возможности программы VisSim. Режимы работы. Структурная устойчивость или неустойчивость некоторых простейших замкнутых линейных систем, упрощенный критерий устойчивости по ЛАЧХ, условие его применимости, связь этого условия с шагом интегрирования при моделировании. Параллельное включение двух звеньев – свойства результирующего звена, свойства а.ч.х. и ЛАЧХ. Разделение движений по двум каналам управления. Разделение движений по двум датчикам с различными шумовыми свойствами в различн, страница 38

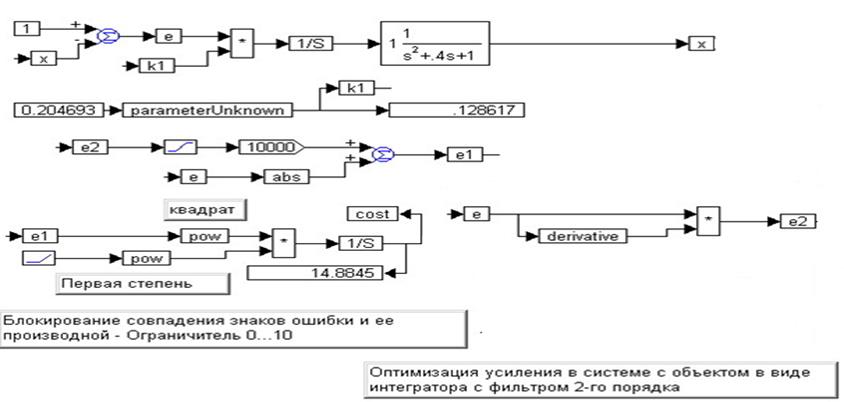
Блокирование перерегулирование более 100,0%:

Применим нелинейность типа «Зона нечувствительности» с шириной 2,002. Т.е. от -1,001 до +1,001. ТОГДА:

4)  Если ошибка лежит в пределах диапазона -100,1%...+100,1%, то на выходе нелинейности – НУЛЬ;

5)  Если ошибка выйдет за диапазон -100,1%...+100,1%, то на выходе возникает НЕНУЛЕВАЯ разница между ошибкой и этой пороговой величиной.

6)  Эту разницу выпрямляем и усиливаем, например, в 1000 раз, и прибавляем к модулю ошибки.

Как следствие – блок оценки стоимостной функции вырабатывает величину, которая резко возрастает за счет этой добавки. Стоимостная функция резко растет в случае невыполнения требований по ограниченному значению перерегулирования. Следовательно, а этом направлении итерация коэффициентов далее не идет. Как результат, скорость и эффективность процедуры оптимизации возрастает.

ЦЕЛЕСООБРАЗНО ОГРАНИЧИТЬ ПЕРЕРЕГУЛИРОВАНИЕ даже не величиной 100%, а ЛЮБОЙ НАПЕРЕД ЗАДАННОЙ ВЕЛИЧИНОЙ. В этом случае ограничение диапазона поиска коэффициентов ПИД-регулятора уже не столь необходимо.

Для ограничения перерегулирования достаточно осуществить такое преобразование ошибки, при котором попадание ее за допустимый интервал дало бы резкое увеличение стоимостного функционала. Пусть тестовый сигнал всегда единичный (V=1), а допустимая величина перерегулирования задана в виде G% (в процентах по отношению к начальной ошибке), то следует установить для выходной величины X(t) верхний предел

Z=1+G/100.

(Например, при G=10% получаем Z=1.2)

Ситуация X(t)>Z должна резко увеличивать стоимостный функционал.

Для этого достаточно из выходной величины вычесть этот уровень, X₁(t)=X(t)-Z, результат ограничить снизу нулем, X₂(t)=max{0, X₁(t)}, после чего умножить на большой коэффициент и прибавить к модулю ошибки управления, входящей в стоимостный функционал:

e₁(t)=e(t)+X₂(t)

Ошибку e₁(t) далее используем вместо e(t)

72.Особенности синтеза дискретных (цифровых) систем автоматического регулирования в двух случая: 1) частота следования отсчетов удовлетворяет требованиям теоремы Котельникова; 2) это требование не выполняется.

Шаг интегрирования следует выбирать таким, чтобы приращение между двумя соседними точками было пренебрежимо малым. В противном случае интегрирование будет осуществляться некорректно. 

В результате квантования сигнала по времени при дискретном представление сигнала может произойти потеря информации, так как остаются значения сигнала только в дискретные моменты времени. Однако благодаря одному из свойств реальных систем в них при определенных условиях сохраняется полная информация о сигнале, если последний известен, лишь в дискретные моменты времени. Это свойство известно как теорема Котельникова: непрерывный сигнал можно полностью отобразить и точно воссоздать по последовательности измерений или отсчетов величины этого сигнала через одинаковые интервалы времени, меньшие или равные половине периода максимальной частоты, имеющейся в сигнале.

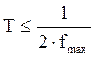 - аналитическое представление теоремы Котельникова, где = /2

Смысл теоремы Котельникова состоит в том, что, если требуется передавать сигнал, описываемый функцией с ограниченным спектром, то достаточно передавать отдельные мгновенные значения, отсчитанные через конечный промежуток времени T . По этим значениям непрерывный сигнал может быть полностью восстановлен на выходе системы (рис. 1).

При соблюдение условий теоремы Котельникова параметры системы (качество переходного процесса) будет определяться настройкой регулятора, свойствами самого объекта. При несоблюдение сигнал будет получен с потерей информации о нем (рис. 2). При этом ЦАП не сможет адекватно реагировать на его изменения, т.к. не будет точного значения сигнала. Для подавления высокочастотной составляющей сигнала в цифровых системах должны использоваться аналоговые фильтры.

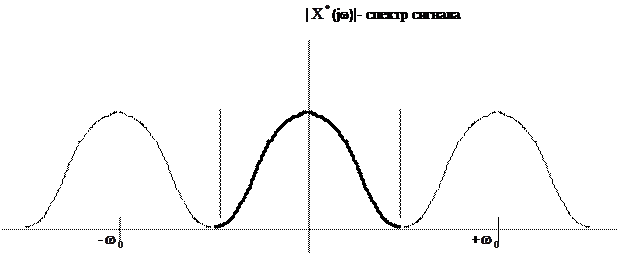Рис. 1

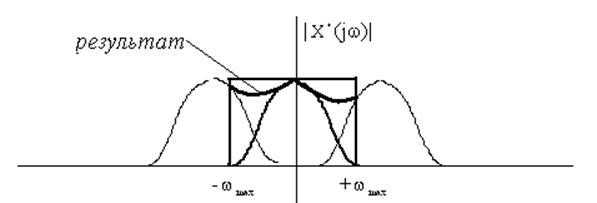
Рис.2