2) обоснованность целевых функционалов – такое их формулирование, при которых достижение их минимума гарантирует наилучшее соответствие свойств замкнутой системы предъявляемым к ней техническим требованиям;
3) корректность методик моделирования и оптимизации
Поиск «оптимальной настройки» ПИ регулятора для системы первого порядка или ПИД-регулятора для системы, представленной уравнением второго порядка – задача не корректная, в смысле отсутствия экстремума любого стоимостного функционала от настраиваемых параметров.
На практике же для любого без исключения объекта всегда существует наилучшая настройка. Это связано с тем, что не существует идеальных объектов ни первого, ни какого-либо конечного порядка в неограниченном диапазоне частот и без учета ограничений входного воздействия. Именно эти ограничения приводят к оптимальности на практике определенных параметров регулятора. Существование оптимального решения вызвано ограниченностью достижимого быстродействия и качества переходного процесса.
Другой причиной может являться транспортное запаздывание в модели реального объекта. В реальном объекте присутствуют все эти причины в совокупности и некоторые другие, но которая из них начинает сказываться раньше, зависит от соотношения соответствующих величин в истинном математическом описании объекта. Поскольку именно эти «нюансы» определяют оптимальность настройки, то модель, не учитывающая этих особенностей не пригодна для отыскания не только оптимального решения, но и вообще не пригодна для решения поставленной задачи
Поэтому некорректно было бы тем или иным способом оптимизировать регулятор для идеализированного объекта первого или второго порядка (то есть без учета высших порядков, ограничения управления, запаздывания, нелинейности или еще какой-то хотя бы одной дополнительной особенности объекта).
Если же в реальной задаче управление осуществляется дискретно, и эта величина шага интегрирования войдет в модель объекта или регулятора, то такая задача будет поставлена корректно, но в этом случае мы уже имеем не объект первого или второго порядка, а объект еще и с запаздыванием.
Проверка обоснованности модели и корректности моделирования может быть осуществлена критерию: переходные процессы в модели и в практической системе должны совпадать при оптимальных настройках, а также в случае, когда в оптимальном регуляторе несущественно меняются по
Оптимизация модели заключается в таком подборе ее параметров, при котором обеспечивается минимум какой-л. целевой ф-ции.
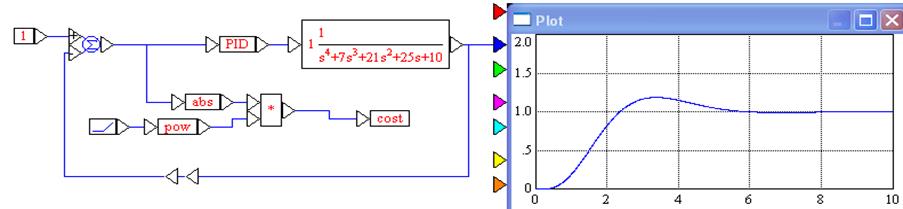
В VisSim она реализуется особым построение модели, в которую включаются специальные блоки для многократного моделирования с изменяемыми параметрами. Изменение параметров производится итерационно. Установку общих параметров оптимизации можно выполнить из окна, вызываемого командой Optimization Properties. В этом окне можно выбрать метод оптимизации, число итераций и допуск ошибки. Для включения оптимизации ставим галочку на Perform Optimization. Блок constraint служит для задания ограничений, используется совместно с блоком unknown для решения неявных уравнений. Блок неизвестных параметров Parameter unknown используется для постановки в блок-схему подбираемых ими параметров, минимизирующих целевую ф-цию. Блок cost служит для задания целевой функции. Он используется оптимизаторами ViSSim для автоматического подбора параметров системы в итерационном процессе. Целевая функция составляется в соответствии с характером решаемой задачи.
Виды оптимизации отличаются по признаку того, как задан критерий качества, и какое соответствие ему следует искать.
Обеспечение минимума/максимума функционала. Основывается на выбранной целевой функции, минимум/максимум которой и следует найти. При такой задаче результат решения задачи определяется методом решения и правильностью выбора целевой функции. Пример(pow=3):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.