Основные особенности и возможности программы VisSim. Режимы работы. Структурная устойчивость или неустойчивость некоторых простейших замкнутых линейных систем, упрощенный критерий устойчивости по ЛАЧХ, условие его применимости, связь этого условия с шагом интегрирования при моделировании. Параллельное включение двух звеньев – свойства результирующего звена, свойства а.ч.х. и ЛАЧХ. Разделение движений по двум каналам управления. Разделение движений по двум датчикам с различными шумовыми свойствами в различн, страница 33

56.Чем аналитическое решение замкнутой системы отличается от решения методом интегрирования? Принципиально ли это отличие? Обосновать.

Теоретически, когда система абсолютно линейна, можно перестанавливать без проблем. При аналитическом решении тоже (пользуемся правилами структурных преобразований схем). При моделировании может влиять, т.к. каждый элемент имеет свой шаг (на самом деле - запаздывание). Но в пределах корректных схем влиять не должно только для линейных систем. На практике влияет всегда. На практике невозможно просто так взять и поменять местами.

Аналитически могут сократиться два сомножителя или поглотить друг друга. Тогда они не будут входить в результат. При моделировании каждый будет моделироваться, и иметь задержку. Может оказаться, что один из них нереализуем физически (звенья предугадывания и запаздывания).

57.Могут ли быть решены замкнутые системы, содержащие передаточные функции со степенью числителя, большей степени знаменателя, аналитически? Могут ли они быть решены методом моделирования (численным интегрированием)? Могут ли они быть реализованы физически?

Аналитически можно решить.

Методом моделирования нельзя, пакеты моделирования не позволяют задавать такие звенья.

Ни один реальный объект не может описываться линейной моделью, где степень числителя больше степени знаменателя или даже хотя бы равна ему.

Однако VisSim позволяет задать структуру вида

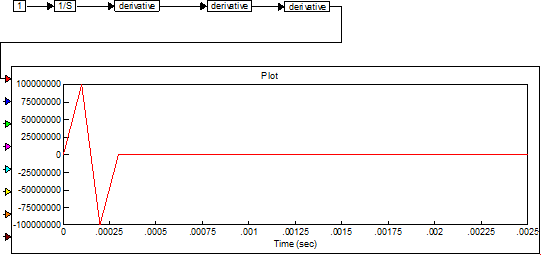
На практике таких систем не существует.

58.Могут ли быть решены замкнутые системы, содержащие передаточные функции в виде экспоненты от s с положительным (отрицательным) коэффициентом, методом моделирования (численным интегрированием)? Могут ли они быть решены методом моделирования (численным интегрированием)? Могут ли они быть реализованы физически?

Экспонента с положительной степенью чисителя представляет собой звено предугадывания и на практике нереализуемо! При попытки моделирования такого звена, любое адекватное ПО должно выдать ошибку или же вообще не позволить задать положительный коэффициент.

Экспонента с отрицательной степенью числителя это звено транспортной задержки (запаздывания). Запаздывание характерно для всех реальных объектов. Такое звено обязательно для пакетов моделирования динамических систем. Оно как существует физически, так и может быть смоделировано.

Если моделировать систему, содержащую звено предугадывания,  то возникнет ошибка сумматора или сообщение об ошибке. Постоянная звена delay положительна. Это значит, что на вход t надо подавать положительную константу, тогда будем моделировать звено задержки. Если константа < 0, то звено предугадывания.

59.Влияет ли (всегда, иногда, никогда) перестановка элементарных звеньев на итоговую модель объекта теоретически, при аналитическом решении, при моделировании, в практических системах?

Теоретически, когда система абсолютно линейна, можно перестанавливать без проблем. При аналитическом решении тоже (пользуемся правилами структурных преобразований схем). При моделировании может влиять, т.к. каждый элемент имеет свой шаг (на самом деле - запаздывание). Но в пределах корректных схем влиять не должно только для линейных систем. На практике влияет всегда. На практике невозможно просто так взять и поменять местами.

Если система нелинейная, то ни о какой перестановке не может быть и речи.

При моделировании:

Аналитически могут сократиться два сомножителя или поглотить друг друга. Тогда они не будут входить в результат. При моделировании каждый будет моделироваться, и иметь задержку. Может оказаться, что один из них нереализуем физически (звенья предугадывания и запаздывания).

60.Может ли система без интегратора в прямом контуре иметь строго нулевую ошибку при моделировании, при аналитическом решении, на практике?

Ни при моделировании, ни при аналитическом решении, ни на практике строго нулевую ошибку система иметь не может без интегратора.