Если нет интегратора и в объекте, и в регуляторе, то нулевая ошибка не получится аналитически и при моделировании. На практике всегда есть ошибка, значения меньше которой мы уже считаем 0 (например ошибка датчика). Ошибка менее чем допустимая по ТЗ на практике уже считается нулем.
Интегратор необходим для устранения статической ошибки.
Дифференциатор нужен для местного подъема ФЧХ, если это поможет. Если объект второго порядка и резко переходит из нулевого порядка во второй, то эффективнее им управлять применением дифференцирования.
Два интегратора необходимо для более эффективного роста точности с падением частоты. Это как раз достигается более резким ростом значения а.ч.х с движением в область нулевых частот, что дает только двойной интегратор. Полезные свойства второго порядка интегратора состоят в уменьшение ошибки при отработке линейно-нарастающего управляющего воздействия или при подавление линейно нарастающей помехи. Это экзотический случай. Применяется в системах с астатизмом второго порядка (например, угол поворота антенны, следящие системы).
Два дифференциатора – экзотика. Применяется крайне редко, если есть очень большой участок третьего порядка и мало шумов.
Дан характеристический полином вида
PN(s) = 1 + a1 s + a2 s2 + … sN. (2.2)
Для моделирования фильтра запишем его уравнение в следующем виде:
 (2.3.)
(2.3.)
Если дана передаточная функция, её сразу можно забить в блок Transfer Function, или преобразовать к виду (2.3) и построить систему на интеграторах.
где V – вход фильтра, Y – выход фильтра.
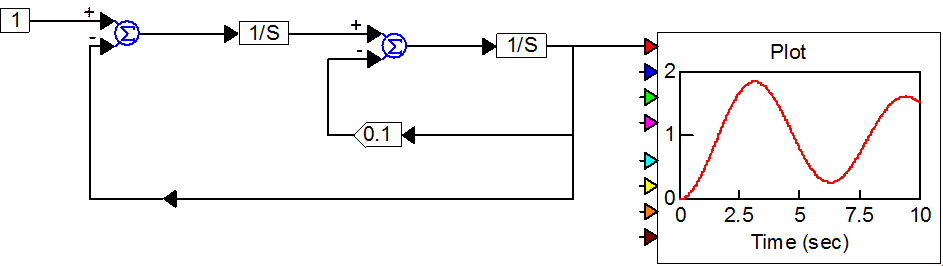
Дан характеристический полином вида
PN(s) = 1 + a1 s + a2 s2 + … sN. (2.2)
Для моделирования фильтра запишем его уравнение в следующем виде:
 (2.3.)
(2.3.)
Если дана передаточная функция, её сразу можно забить в блок Transfer Function, или преобразовать к виду (2.3) и построить систему на интеграторах.
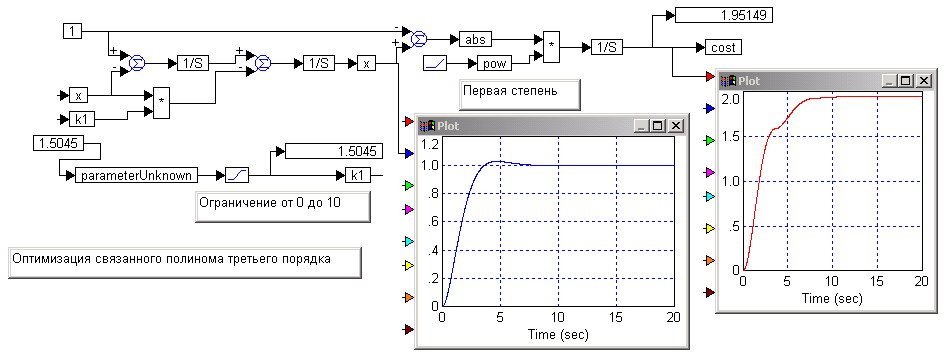
Под постановкой задачи оптимизации понимается:
1) обоснованность математической модели объекта - задание ее с такой степенью подробности, при которой теоретически оптимальный регулятор совпадает с практически оптимальным;
2) обоснованность целевых функционалов – такое их формулирование, при которых достижение их минимума гарантирует наилучшее соответствие свойств замкнутой системы предъявляемым к ней техническим требованиям;
3) корректность методик моделирования и оптимизации
На рисунке представлена система второго порядка с передаточной функцией
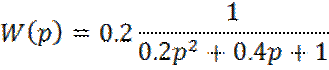
и ПИД – регулятором. В систему введено звено запаздывания, составляющее 0,5 с. Целевая функция – интеграл от квадрата ошибки.
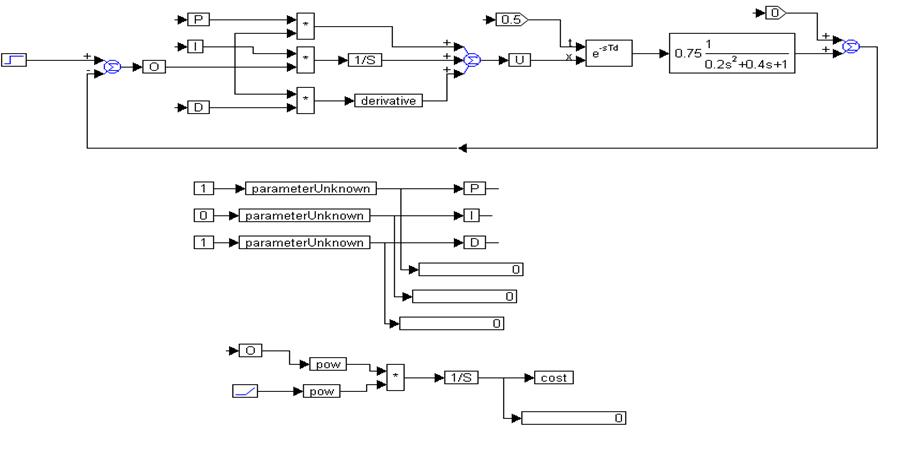
Проверка обоснованности модели и корректности моделирования может быть осуществлена по следующему критерию: переходные процессы в модели и в практической системе должны совпадать при оптимальных настройках, а также в случае, когда в оптимальном регуляторе несущественно меняются по очереди различные коэффициенты.
Из теории автоматического управления неявно следует невозможность отыскания оптимального ПИД-регулятора для объекта второго порядка, так же как невозможность отыскания оптимального ПИ-регулятора (а также П-регулятора) для идеального объекта первого порядка. Отсутствие оптимального решения не говорит о невозможности решения задачи, а означает, что какое бы решение мы не отыскали, всегда остается указать другое решение, которое будет лучше по используемым критериям
Под постановкой задачи оптимизации понимается:
2) обоснованность математической модели объекта - задание ее с такой степенью подробности, при которой теоретически оптимальный регулятор совпадает с практически оптимальным;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.