


























































Балтийский Государственный Технический Университет «Военмех»
Лекции по механике полёта.
Выполнили: Архипова И. А.
Захаров А. В.
Группа И321
Преподаватель: Санников В.А.
2005г
Используемые сокращения:
ЛА – летательный аппарат
ПФ – передаточная функция
c.к. – система координат ц.м. – центр масс т.к. – так как т.д. – так далее т.е. – то есть
08.02.05 *
Введение.
Летательный аппарат (ЛА) может рассматриваться как некоторая динамическая система. При проектировании возникает задача оценки качества этой системы, которое может производиться экспериментальными или теоретическими методами исследования. В случае теоретических методов необходимо составить математическую модель управляемого движения ЛА. Математическая модель - это совокупность уравнений, позволяющая определить параметры движения при заданных начальных условиях и определённых управляющих и возмущающих воздействиях.
Процесс создания математической модели (процесс алгоритмизации) можно представить состоящим из следующих этапов:
1. Математическое описание движения управляемого ЛА.
2. Математическая формулировка целей управления (критериев оптимальности).
3. Количественная характеристика взаимодействия ЛА с окружающей средой (силы и моменты, действующие на ЛА в полёте).
4. Математическое описание алгоритма управления (закон управления).
5. Математическое описание схемы технической реализации алгоритма управления.
Наиболее общей формой математической модели является система нелинейных дифференциальных уравнений, содержащая в своей структуре случайные факторы. На определенных стадиях проектирования могут использоваться математические модели детерминированные (не содержащие случайных факторов). И при этом в зависимости от характера исследуемой задачи могут учитываться упругость конструкции ЛА, колебание жидкого наполнения, наличие подвижных масс («маховиков») внутри ЛА. Определенная специфика при составлении математической модели должна учитываться при движении ЛА в воде.
Глава 1.
Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения.
Полная система уравнений, из которых состоит эта модель, включает:
1. Динамические уравнения движения пространственного движения ЛА.
2. Кинематические соотношения, связывающие линейные или угловые скорости ЛА с линейными или угловыми координатами.
3. Уравнения, описывающие изменение массы и моментов инерции ЛА.
4. Геометрические и вспомогательные соотношения (уравнения связи между различными системами координат, соотношения между углами, определяющими ориентацию ЛА в различных системах координат, явные выражения для сил, моментов и т.д.).
Будем рассматривать случай движения ЛА в воздухе вблизи поверхности земли. Для рассмотрения этого движения используются различные системы координат, чаще всего декартовые (то есть прямоугольные).
Системы координат. Геометрические и кинематические соотношения.
Все системы координат декартовые и правые:
1.
Стартовая с.к. (земная) ![]()
2.
Связанная с.к. ![]()
3. Скоростная с.к. Oxyz
4.
Полусвязанная с.к. ![]()
5.
Полускоростная с.к. ![]()
![]() - точка старта, расположена на поверхности земли
- точка старта, расположена на поверхности земли
O – центр масс ЛА
1. Стартовая с.к. принимается
инерциальной, связанной с неподвижной землёй. Ось![]() направлена
по направлению стрельбы,
направлена
по направлению стрельбы, ![]() ;
; ![]() - плоскость стрельбы,
- плоскость стрельбы, ![]() - горизонтальная плоскость.
- горизонтальная плоскость.
2. Связанная с.к. неизменно связана с ЛА как с твёрдым телом. Движение этой системы в пространстве воспроизводит пространственное движение ЛА. Если рассматривать ЛА как недеформируемое твёрдое тело, то в пространственном движении он имеет 6 степеней свободы, из которых 3 степени свободы определяют вращательное движение относительно центра масс, 3 степени свободы – движение центра масс.
Во вращательном движении имеет 3 степени свободы.
![]() -
совпадает с осью ЛА и направлена от ц.м. к носику. Если ЛА представляет
летающее крыло, то направлена по хорде крыла.
-
совпадает с осью ЛА и направлена от ц.м. к носику. Если ЛА представляет
летающее крыло, то направлена по хорде крыла.
![]() и лежит
в плоскости симметрии
и лежит
в плоскости симметрии
![]() -
плоскость симметрии, если ЛА выполнен по самолётной схеме;
-
плоскость симметрии, если ЛА выполнен по самолётной схеме; ![]() лежит в некоторой фиксированной
относительно ЛА плоскости, если ЛА представляет собой баллистическую ракету.
лежит в некоторой фиксированной
относительно ЛА плоскости, если ЛА представляет собой баллистическую ракету.
![]() и даёт
правую систему.
и даёт
правую систему.
3. Скоростная с.к. oxyz. Во вращательном движении относительно ц.м. также, как и связанная, имеет 3 степени свободы.
х совпадает с ![]() (вектором скорости ц.м.)
(вектором скорости ц.м.)
![]() и лежит
в плоскости симметрии (
и лежит
в плоскости симметрии (![]() )
)
4-ая и 5-ая с.к. во вращательном движении имеют 2 степени свободы.
4. Полусвязанная с.к.
![]() совпадает
с осью ЛА
совпадает
с осью ЛА ![]()
![]() и лежит
в вертикальной плоскости, проходящей через ось
и лежит
в вертикальной плоскости, проходящей через ось![]() (ось
ЛА)
(ось
ЛА)
5. Полускоростная с.к.
![]() совпадает
с осью х (
совпадает
с осью х (![]() )
)
![]() и лежит
в вертикальной плоскости, проходящей через вектор скорости ц.м.
и лежит
в вертикальной плоскости, проходящей через вектор скорости ц.м.
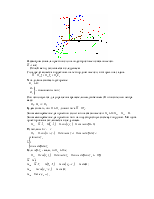
1. Взаимное расположение стартовой, связанной и полусвязанной с.к. при совмещённых началах.
Совместим точку старта с ц.м.
Оx0y0z0
Ox1y1z1
Ox2y2z2
Точка О – ц.м. ЛА
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.