|
Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф.Устинова Кафедра систем обработки информации и управления (И3) |
|
|
Лабораторная работа №3 Дисциплина: “Механика полёта” Тема: “Рассмотрение режимов СН в вертикальной плоскости.” |
|
|
Преподаватель: Александров А.А. Студент: Фомин Святослав Группа И-391 Вариант 10 |
|
|
Санкт-Петербург 2013 год |
|
Цель работы: исследование различных законов СН.
Рассматривается процесс СН в вертикальной плоскости.
Заданы начальные условия положения ЛА и Ц :
х = 12000, y = 600 м, V = 257 м/с, хц = 14000м, уц = 900 м.
Система уравнений движения центра масс ЛА в вертикальной плоскости (уравнения продольного движения и Ц):
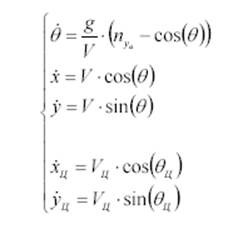
Уравнения связи имеют вид:
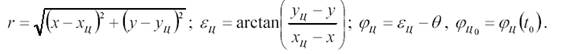
ny=1
Данные по варианту:
Θ(t0) = 0;0.2 рад
Θц(t0) =0 рад
Vц(t0) = 31 м/c
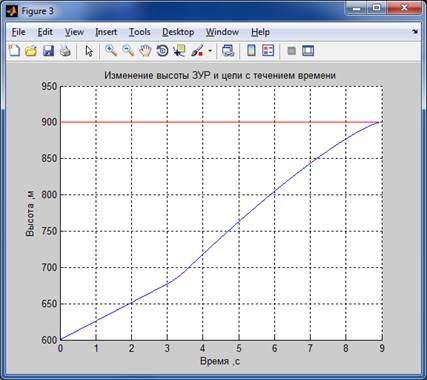
Результаты моделирования:
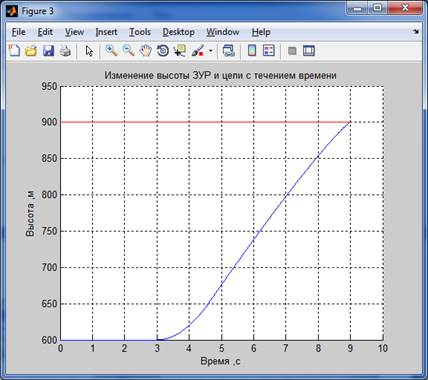
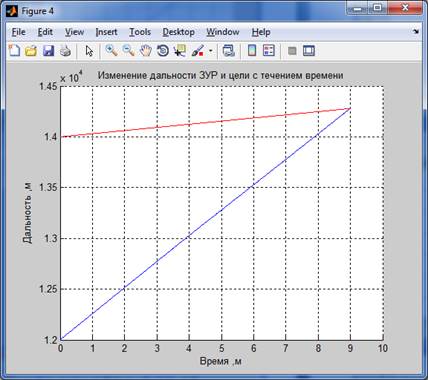
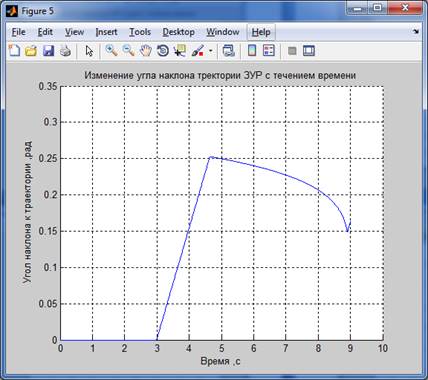
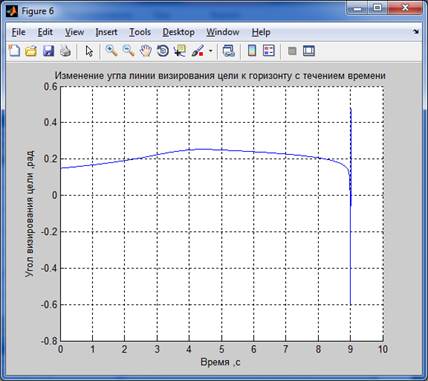
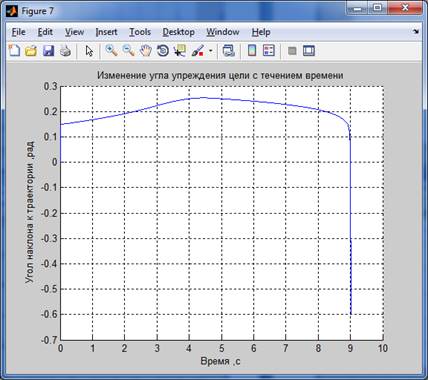
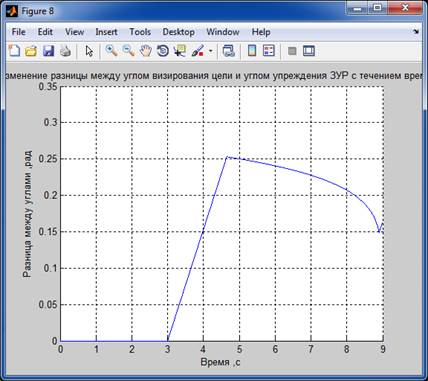
Для 2-го способа :
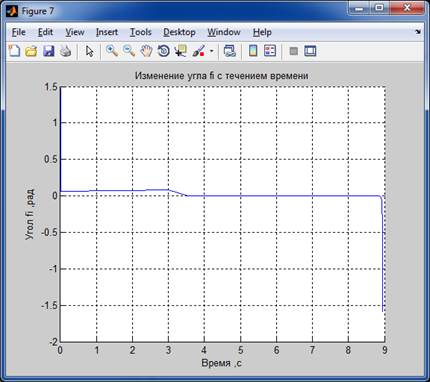
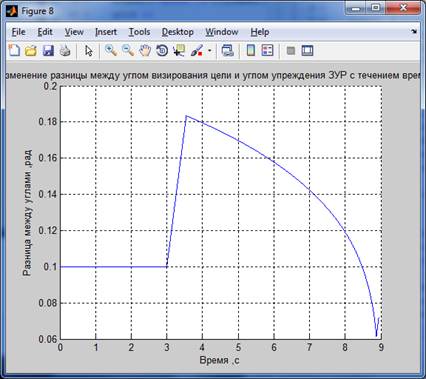
Файл Lab3_1.m
% Лабораторная работа №3
%Самонаведение в вертикальной плоскости
% Вариант 10
%%%%%%%%%%%%%%Координаты и Скорости %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x=12000; % x-coord object ,m
y=600; % y-coord object , m
V=257; % V-object , m\s
xc=14000; % x-coord target , m
yc=900; % y-coord target , m
Vc=31; % V-target (t0) , m\s
g=9.81;
%%%%%%%%%%%Начальные значения углов и константы времени%%%%%%%%%%%%%
ttc=0; % Tetta-target(t0) , rad
tt0=0.0; % Tetta(t0), rad
dt=0.01; % Шаг интегрирования
tf=200; % Время работы программы (или ХИТ в ЗУР)
tl= 3; % Время полета ракеты с выключенной ГСН
t=[0:dt:tf];
n=0; % угол упреждения
DeltaTT=0;
nymax=5;
%%%%%%%%%%%%%% Уравнения связи %%%%%%%%%%%%%%
r(1)=sqrt((x-xc)^2+(y-yc)^2); % Расстояние до цели
fic(1)=atan((yc-y)/(xc-x)); % Линия визирования цели
tt(1)=tt0; % Касательная к траектории - т.к. прямолин движ
for i=1:length(t)
%Углы расстояние до цели
r(i+1)=r(i)+(-V*cos(fic(i)-tt(i))+Vc*cos(fic(i)-ttc))*dt;
fic(i+1)=fic(i)+(V*sin(fic(i)-tt(i))-Vc*sin(fic(i)-ttc))/r(i)*dt;
n(i+1)=fic(i)-ttc; % Угол упреждения
if i<tl/dt
tt(i+1)=tt0; % Полет с отключенной ГСН
else
tt(i+1)=fic(i+1);% Т.к. метод погони
end;
DeltaTT(i+1)=(tt(i+1)-tt(i))/dt;
%Координаты ЗУР
x(i+1)=x(i)+V*cos(tt(i))*dt;
y(i+1)=y(i)+V*sin(tt(i))*dt;
%Координаты цели
xc(i+1)=xc(i)+Vc*cos(ttc)*dt;
yc(i+1)=yc(i)+Vc*sin(ttc)*dt;
%Перегрузка ЗУР
ny(i+1)=abs((V*DeltaTT(i+1))/g+cos(tt(i)));
if ny(i+1)>nymax
tt(i+1)=tt(i)+g*(nymax-cos(tt(i)))/V*dt;
DeltaTT(i+1)=(tt(i+1)-tt(i))/dt;
ny(i+1)=abs((V*DeltaTT(i+1))/g+cos(tt(i)));
end;
%Выход из цикла
if (r(i)<r(i+1))||r(i)<0||y(i)<0
tkon=t(i); %Время перехвата
rk=sqrt((x(i)-xc(i))^2+(y(i)-yc(i))^2);; % Промах
fprintf('вpeмя перехвата: %4.4f , промах: %1.4f \n\n',tkon,rk);
break
end
end;
t=[0:dt:tkon+1*dt]; ny(i+1)=ny(i);% магия
Файл lab3_2.m
% Лабораторная работа №3
%Самонаведение в вертикальной плоскости
% Вариант 10
%%%%%%%%%%%%%%Координаты и Скорости %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x=12000; % x-coord object ,m
y=600; % y-coord object , m
V=257; % V-object , m\s
xc=14000; % x-coord target , m
yc=900; % y-coord target , m
Vc=31; % V-target (t0) , m\s
g=9.81;
%%%%%%%%%%%Начальные значения углов и константы времени%%%%%%%%%%%%%
ttc=0; % Tetta-target(t0) , rad
tt0=0.1; % Tetta(t0), rad
dt=0.01; % Шаг интегрирования
tf=200; % Время работы программы (или ХИТ в ЗУР)
tl= 3; % Время полета ракеты с выключенной ГСН
t=[0:dt:tf];
n=0; % угол упреждения
DeltaTT=0;
nymax=5;
%%%%%%%%%%%%%% Уравнения связи %%%%%%%%%%%%%%
r(1)=sqrt((x-xc)^2+(y-yc*(1+rand(1)*0.1))^2); % Расстояние до цели
fic(1)=atan((yc*(1+rand(1)*0.1)-y)/(xc-x)); % Линия визирования цели
tt(1)=tt0; % Касательная к траектории - т.к. прямолин движ
for i=1:length(t)
%Углы расстояние до цели
r(i+1)=r(i)+(-V*cos(fic(i)-tt(i))+Vc*cos(fic(i)-ttc))*dt;
fic(i+1)=fic(i)+(V*sin(fic(i)-tt(i))-Vc*sin(fic(i)-ttc))/r(i)*dt;
n(i+1)=fic(i)-ttc; % Угол упреждения
if i<tl/dt
tt(i+1)=tt0; % Полет с отключенной ГСН
else
tt(i+1)=fic(i+1);% Т.к. метод погони
end;
DeltaTT(i+1)=(tt(i+1)-tt(i))/dt;
%Координаты ЗУР
x(i+1)=x(i)+V*cos(tt(i))*dt;
y(i+1)=y(i)+V*sin(tt(i))*dt;
%Координаты цели
xc(i+1)=xc(i)+Vc*cos(ttc)*dt;
yc(i+1)=yc(i)+Vc*sin(ttc)*(1+rand(1)*0.1)*dt;
%Перегрузка ЗУР
ny(i+1)=abs((V*DeltaTT(i+1))/g+cos(tt(i)));
if ny(i+1)>nymax
tt(i+1)=tt(i)+g*(nymax-cos(tt(i)))/V*dt;
DeltaTT(i+1)=(tt(i+1)-tt(i))/dt;
ny(i+1)=abs((V*DeltaTT(i+1))/g+cos(tt(i)));
end;
%Выход из цикла
if (r(i)<r(i+1))||r(i)<0||y(i)<0
tkon=t(i); %Время перехвата
rk=sqrt((x(i)-xc(i))^2+(y(i)-yc(i))^2); % Промах
fprintf('вpeмя перехвата: %4.4f , промах: %1.4f \n\n',tkon,rk);
break
end
end;
t=[0:dt:tkon+1*dt]; ny(i+1)=ny(i);% магия
Промах ( для метода №2) = 0,2866 Промах (для метода №1)=0,5846
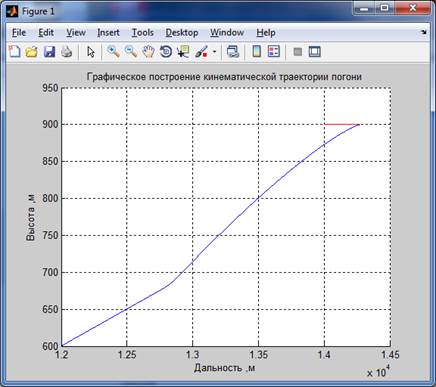
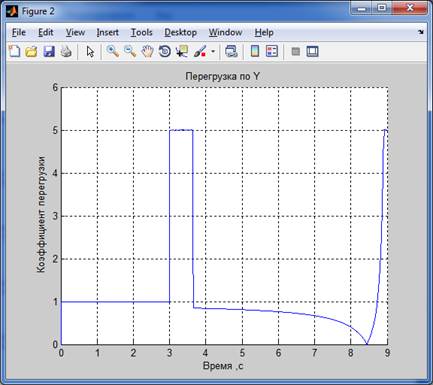
Траектория полета и перегрузка по Y для способа 1 (ny_max=5)
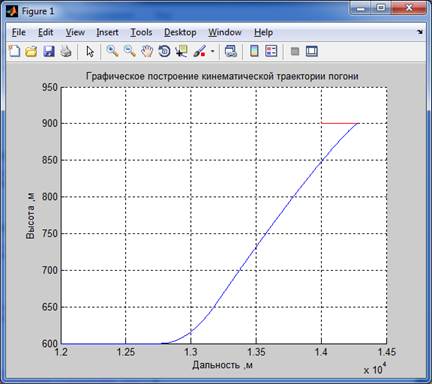
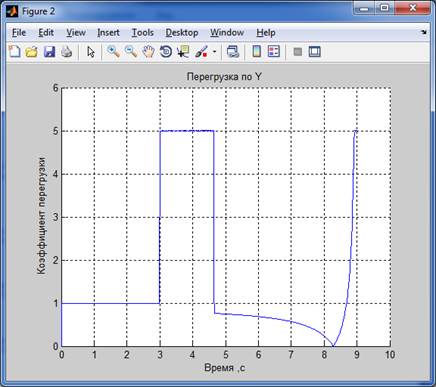
Траектория полета и перегрузка по Y для способа 2 (ny_max=5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.