Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения, страница 15

α  

α

τ

 =  – α

Rcosα ≈ R

Rsinα ≈ Rα

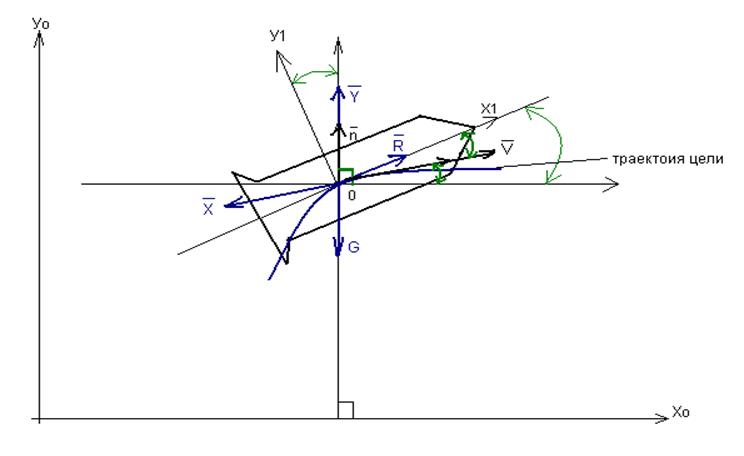
Плоско-параллельное движение состоит из движения центра масс и вращения. Боковое движение описывается 3-им, 4-ым, 5-ым, 7-ым, 8-ым, 12-ым, 14-ым и 15-ым уравнениями системы (I). При малых α, β, γ, γ_с, ω_х1, ω_у1, ω_z1, уравнения бокового движения будут иметь вид:

1)  mvcos (dΨ/dt) = Rβ + Z

2)  J_X1(dω_х1/dt) = M_RX1 + M_AX1

3)  J_Y1(dω_y1/dt) = M_RY1 + M_AY1

4)  (dΨ/dt) = (1/cos)ω_у1

5)  (dγ/dt) = ω_х1 - ω_у1tg                                                                (III)

6)  (dz₀/dt) = - Vcos sinΨ

7)  sinΨ cos = sinΨ cos + αsinΨ – βcosΨ

8)  γ_с cos = βsin + γ cos

Эту систему обозначим (III).

Параметры бокового движения Ψ, φ, β, γ, γ_с, ω_х1, ω_у1, ω_z1, z₀ при известных δ_н и δ_э.

Уравнения бокового движения (III) зависят от параметров продольного движения, поэтому боковое движение может существовать только вместе с продольным. Уравнения бокового движения можно решать после того, как будут определены параметры продольного движения. Таким образом, вместо системы (I) мы получили две системы (II) и (III) более низкого порядка, которые интегрируются последовательно. Сначала интегрируется система (II), а потом (III).

Боковое движение состоит из движения рысканья и движения крена. Движение рысканья определяется 1-ым, 3-им, 4-ым, 6-ым, 7-ым уравнениями системы (III).

Движение крена определяется 2-ым, 5-ым и 8-ым уравнениями системы (III).

Эти движения в общем случае связаны, однако во многих практических случаях эти движения можно рассматривать независимо друг от друга. Часто используется допущение, что движение рысканья слабо зависит от параметров движения крена. И уравнения рысканья можно решать независимо от уравнений, описывающих движение крена (не учитывать перекрестную аэродинамическую связь между движением рысканья и крена). Уравнения движения крена более существенно зависят от параметров движения рысканья и их можно рассматривать после того, как движение рысканья определено.

Линеаризация общей пространственной системы.

Это один из самых распространенных способов упрощения сложной системы нелинейных уравнений (I). Для проведения линеаризации необходимо, чтобы было известно некоторое невозмущенное программное движение ЛА (требуемое движение). Параметры невозмущенного движения определяют обычно приближенно, с помощью численного интегрирования дифференциальных уравнений этого движения или иным способом, в зависимости от характера рассматриваемой задачи. Кроме того, необходимо, чтобы параметры действительного движения отличались от параметров невозмущенного на некоторые малые величины, которые называются отклонениями или вариациями. Предположим далее, что существуют первые частные производные от правых частей дифференциальных уравнений по всем входящим в них параметров. Линеаризация производится с использованием метода малых возмущений. Коротко остановимся на существе этого метода.

29.03.05 *

Пусть некоторая динамическая система описывается нелинейной системой дифференциальных уравнений, которую представим в нормальной форме Коши:

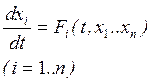                                                                                                               (1)

Пусть известно некоторое программное (невозмущённое) движение этой системы. Параметры этого движения обозначим . Действительное движение отличается от невозмущённого, т.к. на систему действуют возмущающие силы, точно учесть которые невозможно. Предположим, что отклонения параметров от невозмущённых   являются малыми возмущениями:

                                                                                                     (2)

Подставляем (2) в (1):

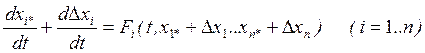
Правые части разложим в ряд Тейлора в окрестности невозмущённого движения. Ограничимся членами разложения, которые содержат отклонения  (вариации) в степени не выше первой.

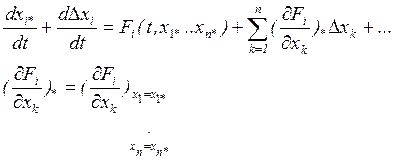
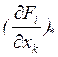 - значения частных производных, отвечающие невозмущённому движению.

Т.к.  является решением системы (1), то справедлива следующая система: