Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения, страница 6

25.02.05

 

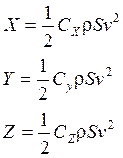
 зависят от числа Маха (М);

 - число Рейнольца (им можно пренебречь);

М=

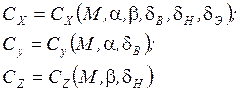
 - угол отклонения рулей направления;

 - угол отклонения рулей высоты;

 - угол отклонения элеронов;

Коэффициенты  определяются экспериментально или путём математического моделирования процесса обтекания ЛА. Существуют также приближённые формулы.

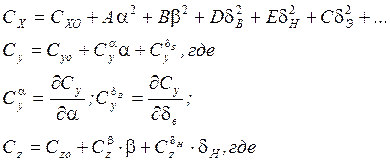
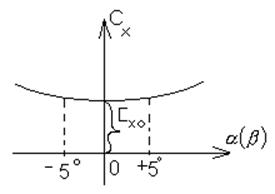
 - значения соответствующих коэффициентов при нулевых угловых параметрах, при этом коэффициенты  и  будут иметь место в том случае, если ЛА аэродинамически несимметричен. Для аэродинамически симметричного аппарата  и  равны нулю.

Можно изобразить следующие графики зависимости :

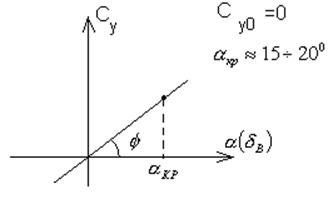
                                                                       tg - угловой коэффициент                    

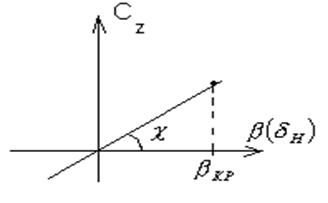
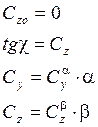
Подъёмная сила от  зависит значительно меньше, чем от , кроме случая ЛА с поворотным крылом.

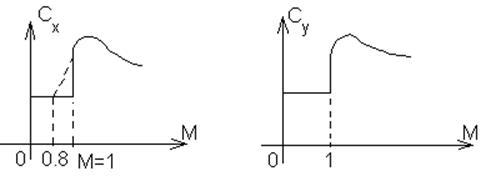
В интервале трансзвуковых скоростей М(0,8-1,2).

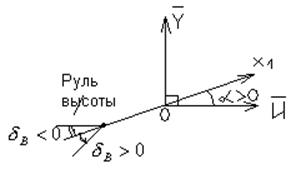
Правило знаков:

Угол атаки >0, если У направлено вверх. Угол отклонения руля >0, если отсчёт производится от нейтрального положения против часовой стрелки.

Используя рис.4, запишем выражение для проекции суммарной аэродинамической  силы на оси полускоростной и связанной системы координат.

Проекции на полускоростные оси:

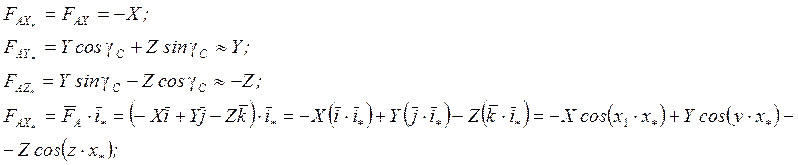
Т.к.  - значит они малые первого порядка.

 мало только тогда, когда крен стабилизирован. Следовательно

Т.к.  - малая величина, то, следовательно

Проекции на связанные оси:

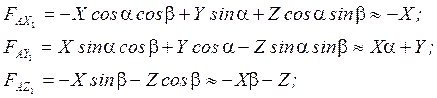
Учитывая малость углов  можно считать, что, следовательно, можно записать:

 

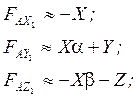
Запишем уравнение поступательного движения ЛА в пространстве в проекциях на полускоростные и связанные оси, учитывая, левые и правые части.

Рассмотрим сначала полускоростную систему координат .

Учитывая малость углов , :

     

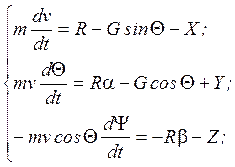
Рассмотрим связанную систему координат .

Учитывая малость углов , запишем:

      

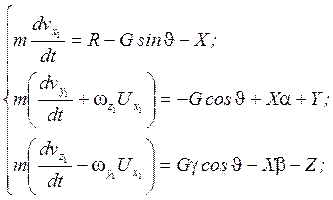
Понятие о маневренности. Выражения для перегрузок.

Маневренность  - это способность управляемого ЛА совершать полёт по криволинейной траектории.

При полёте по криволинейной траектории изменяется угол возвышения (t) и угол курса (t) . Эти углы показаны на рис.2.

Из рис.2 видно, что угол возвышения - это угол между вектором скорости и горизонтальной плоскостью.

Угол курса - это угол между проекцией скорости центра масс на горизонтальную плоскость и плоскостью стрельбы .

Вектором перегрузки   называется отношение вектора ускорения центра масс к ускорению свободного падения, т.е. 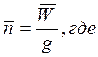   - ускорение центра масс.

Вектор перегрузки можно представить в проекциях на любые оси координат. Чаще всего используются полускоростные оси.

 - направление касательной к траектории;

 - направление нормали к траектории;

 - на бинормаль;

 - нормальная перегрузка.

Запишем выражение для нормальной и касательной перегрузки.

                                  

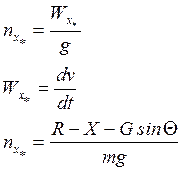
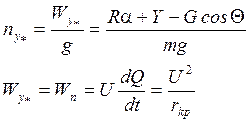
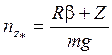
- радиус криволинейной траектории;

Проекции на связанные оси:

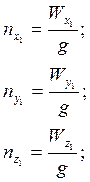
Располагаемая перегрузка - это та часть перегрузки, которую мы можем изменять при управлении.

Запишем формулу для располагаемой нормальной перегрузки:

;

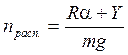Т.к. У=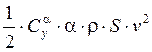, то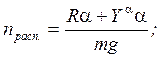 

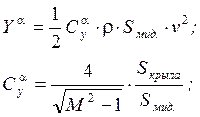
 с подъёмом на высоту уменьшается по экспоненте, а массовая плотность воздуха у земли , где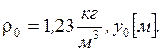

Рули нужны для того, чтобы управлять вращательным движением ЛА.

1.03.05

Уравнение вращательного движения в пространстве.

Выводится с использованием закона моментов количества движения. Закон в векторном виде запишется так:

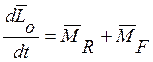      -     закон моментов количества движения               (1)

- момент количества движения относительно центра масс (кинетический момент).

Оно будет иметь смысл, если точка О - неподвижная точка в инерциальном пространстве.

Векторное уравнение (1) будем записывать в проекциях на связанную систему координат. Эта система координат используется преимущественным образом при проектировании уравнения (1). Но на ряду со связанной системой координат, в случае осесимметричного ЛА, может использоваться полусвязанная система координат.

 - связанная система координат;

 - ось симметрии;  

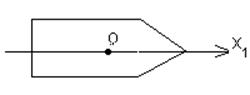
 - полусвязанная система координат;