Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения, страница 4

ЛА в своём пространственном движении имеет 6 степеней свободы, если его рассматривать как недеформируемое твёрдое тело с переменной массой. Его движение определяется 6 обобщёнными координатами: 3 координатами ц.м. и 3 эйлеровыми углами, определяющими угловую ориенмацию ЛА относительно ц.м. . Для определения 6 указанных обобщённых координат нужно составить 6 уравнений динамики. Для вывода этих уравнений используются основные законы механики системы материальных точек и твёрдого тела: закон количества движения и закон моментов количества движения.

18.02.05

1. Изменение вектора количества движения системы в единицу времени равняется главному вектору всех внешних сил, действующих на систему.

=

2. Изменение вектора момента количества движения в единицу времени равно главному моменту всех внешних сил, действующих на систему. При этом вектор момента количества движения и момент внешних сил вычисляются относительно неподвижной точки пространства, или относительно центра масс системы.

- вектор момента количества движения (или кинетический момент);

=

Оба этих закона механики справедливы для тела или системы с постоянной массой.

При этом закон количества движения для тела с постоянной массой трансформируется в уравнение II-го закона механики:   m=,   m=const, 

- абсолютное ускорение;

-скорость центра масс.

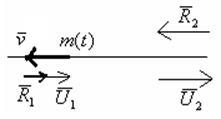
Если масса меняется в зависимости от времени, то эти законы несправедливы. В этом случае появляются дополнительные силы и моменты, вызванные изменением массы. Т.к. поступательное движение может быть описано движением одной точки, совпадающей с центром масс, то для вывода уравнений поступательного движения можно использовать в этом случае уравнение Мещерского:

Уравнение Мещерского описывает движение точки с переменной массой. В общем случае, когда при движении точки с переменной массой имеет место, как отсоединение массы, так и присоединение массы, уравнение Мещерского запишется так:    

m(t) =+  +       

, - реактивные силы (вызваны отсоединением и присоединением массы);

Эти реактивные силы определяются по следующим формулам:

- реактивная сила, вызванная присоединением массы;

_{= ,  где -} секундный приход массы (это количество массы, присоединяющейся в единицу времени);

- относительная скорость присоединения массы;

- реактивная сила тормозит движение точки;

- реактивная сила, вызванная отсоединением массы;

= -Q_{2 ,} где Q₂–секундный расход массы,- относительная скорость отсоединения массы  (скорость истечения продуктов  сгорания из сопла);

Эта сила возникает у ракет с жидкостными, пороховыми двигателями.

Будем считать, что = 0,  =

И будем рассматривать двигатели жидкостные (ЖРД) и пороховые (твердотопливные) (РДТ).

m(t)= +

Обозначим  закон изменения массы следующим образом: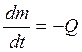

Если Q=const,то (закон изменения массы при постоянном расходе), где - начальная масса точки.

Используя вместо закона количества движения уравнение Мещерского для описания поступательного движения ЛА, мы допускаем некоторую известную неточность, которая происходит оттого, что не учитывается перемещение масс ЛА за счёт выгорания топлива.

Допущение: Поступательное движение ЛА с переменной массой может быть описано уравнением центра масс.

Принимая уравнение Мещерского, видим, что надо учитывать дополнительную реактивную силу, которая обуславливается эффектом отсоединения масс.

Рассмотрим схему ракеты:

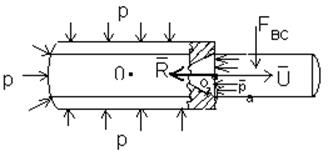
-давление газов на выходе из сопла;

Р ()-атмосферное давление ,зависящее от высоты полёта ;

- площадь выходного сечения;

При движении ЛА в атмосфере  на него будет действовать тяга , приложенная в точке , которая представляет из себя сумму реактивной силы ()  и статической():      

 на выходе сопла не зависит от высоты полёта и всё время постоянно, т.к. внешние возмущения не могут войти в сопло.

На выходе больше скорости звука, т.к. они распространяются со скоростью звука , а на выходе сопла скорость сверхзвуковая.

Скорость звука - это скорость распространения малых возмущений.