19.04.2005 *
Свободная поверхность в невозмущённом состоянии.
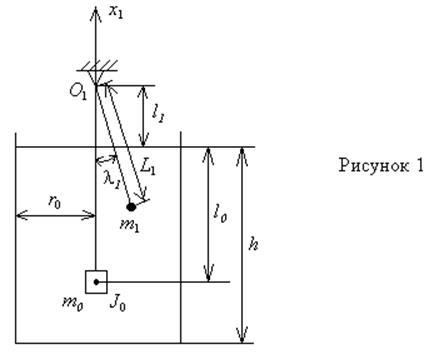
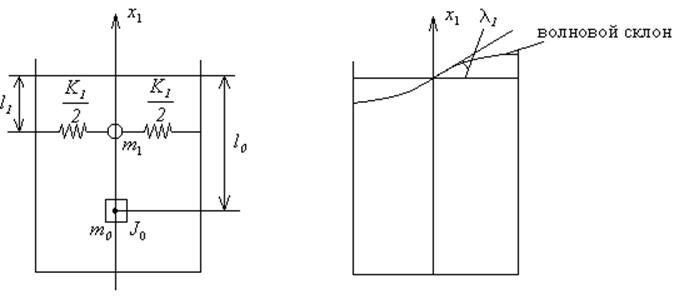
Одна модель (рисунок 1)
представляет собой математический маятник ![]() , точка
подвеса которого принадлежит оси бака и располагается на расстоянии
, точка
подвеса которого принадлежит оси бака и располагается на расстоянии ![]() от свободной поверхности жидкости (
от свободной поверхности жидкости (![]() имитирует массу
жидкости, участвующую в колебаниях 1 тона). Другая модель состоит из массы
имитирует массу
жидкости, участвующую в колебаниях 1 тона). Другая модель состоит из массы ![]() , которая 2 пружинами с жёсткостью
, которая 2 пружинами с жёсткостью ![]() прикреплена к стенкам бака на расстоянии
прикреплена к стенкам бака на расстоянии ![]() от свободной поверхности жидкости. Угол
от свободной поверхности жидкости. Угол ![]() отклонения маятника имитирует наклон
волнового склона в колебаниях 1 тона. Обе механические модели учитывают тот
факт, что часть жидкости не совершает колебаний относительно бака. Масса
отклонения маятника имитирует наклон
волнового склона в колебаниях 1 тона. Обе механические модели учитывают тот
факт, что часть жидкости не совершает колебаний относительно бака. Масса ![]() этой части жидкости жёстко связана со
стенками бака. Считается, что неподвижная часть жидкости имеет относительно
оси, проходящей через центр массы
этой части жидкости жёстко связана со
стенками бака. Считается, что неподвижная часть жидкости имеет относительно
оси, проходящей через центр массы ![]() , момент инерции
, момент инерции ![]() . Как маятниковая, так и пружинно-массовая
модель построены для идеальной, т.е. не имеющей вязкости жидкости, причём
содержащий её бак не имеет каких-либо перегородок. Влияние перегородок сводится
к тому, что всегда имеющаяся у реальной жидкости вязкость будет проявляться в
более сильной степени, приводя к демпфированию свободных колебаний жидкости.
Поэтому при наличии перегородок в механической модели необходимо вводить
жидкостные демферы, при этом остальные параметры модели остаются без изменения.
Коэффициенты, учитывающие демпфирование, могут быть определены только
экспериментально или берутся на основании статистики. Все параметры модели
можно найти в литературе: В.А. Санников, А.С. Шалыгин «Математические модели
динамики полёта ЛА»; Колесников «Жидкостная ракета как объект регулирования».
. Как маятниковая, так и пружинно-массовая
модель построены для идеальной, т.е. не имеющей вязкости жидкости, причём
содержащий её бак не имеет каких-либо перегородок. Влияние перегородок сводится
к тому, что всегда имеющаяся у реальной жидкости вязкость будет проявляться в
более сильной степени, приводя к демпфированию свободных колебаний жидкости.
Поэтому при наличии перегородок в механической модели необходимо вводить
жидкостные демферы, при этом остальные параметры модели остаются без изменения.
Коэффициенты, учитывающие демпфирование, могут быть определены только
экспериментально или берутся на основании статистики. Все параметры модели
можно найти в литературе: В.А. Санников, А.С. Шалыгин «Математические модели
динамики полёта ЛА»; Колесников «Жидкостная ракета как объект регулирования».
Уравнения движения ракеты при учёте колебания жидкости в баках.
Будем рассматривать только продольное движение ракеты. Колебательное движение жидкости будем учитывать только в 1 баке. Используем маятниковую модель колебания жидкости. В этом случае силовое воздействие колеблющейся жидкости на ракету проявляется в силе натяжения маятника, передаваемой на точку подвеса. Для определения этой силы, а также соответствующего момента относительно ц.м. ракеты, нужно рассмотреть колебательное движение маятника, точка подвеса которого не совпадает с ц.м. ракеты и движется с ускорением.
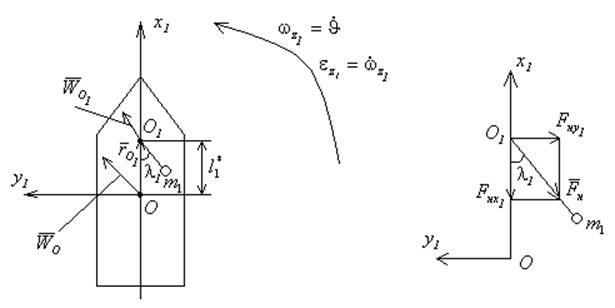
![]()
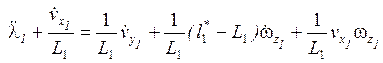 - уравнение колебаний маятника,
точка подвеса которого не совпадает с ц.м. и движется с ускорением
- уравнение колебаний маятника,
точка подвеса которого не совпадает с ц.м. и движется с ускорением
![]() - производные по времени от
проекций скорости ц.м.
- производные по времени от
проекций скорости ц.м. ![]()
При выводе этого уравнения не учитывалось влияние силы веса
маятника ![]() .
.
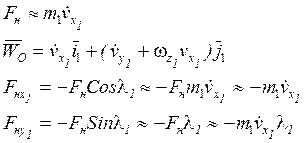
Указанные силы должны быть добавлены в уравнение поступательного движения жёсткой ракеты в вертикальной плоскости.
В уравнение вращательного движения ракеты по
углу тангажа следует добавить момент от силы ![]() .
.
![]()
Момент инерции ![]() неподвижной
части жидкости следует, используя формулу Штейнера, добавить к моменту инерции
ракеты без топлива относительно оси
неподвижной
части жидкости следует, используя формулу Штейнера, добавить к моменту инерции
ракеты без топлива относительно оси ![]() :
:
![]()
![]()
![]() - расстояние между ц.м. ракеты
(точкой О) и ц.м. неколеблющейся жидкости
- расстояние между ц.м. ракеты
(точкой О) и ц.м. неколеблющейся жидкости
![]() - момент инерции неподвижной
части жидкости относительно оси
- момент инерции неподвижной
части жидкости относительно оси ![]() , проходящей через ц.м.
ракеты (точку О)
, проходящей через ц.м.
ракеты (точку О)
Запишем уравнения продольного движения ракеты с учётом колебания жидкости в 1 баке.
Несколько переориентируем связанную с.к.
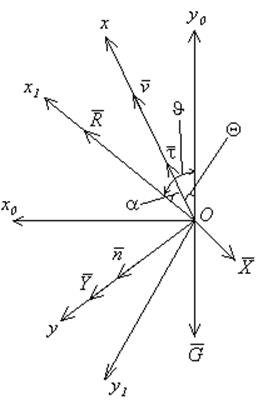
Уравнение движения в вертикальной плоскости:
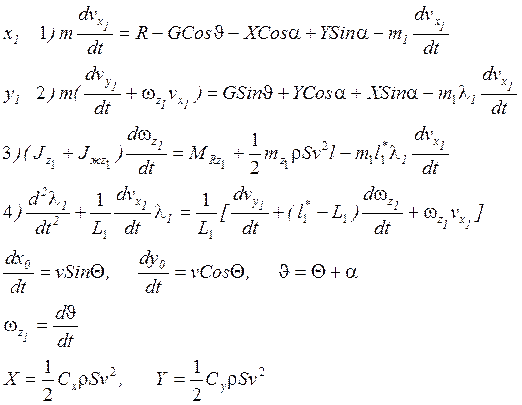
m – масса корпуса и неподвижной части жидкости, не участвующей в колебаниях
![]() - момент инерции ракеты без
топлива, но с маятниками, находящимися в положении равновесия.
- момент инерции ракеты без
топлива, но с маятниками, находящимися в положении равновесия.
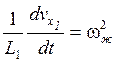 , где
, где ![]() -
собственная частота 1 тона колебаний жидкости в баке.
-
собственная частота 1 тона колебаний жидкости в баке.
22.04.05
Математическая модель пространственного движения ЛА в воде.
Будем рассматривать тело произвольной формы в воде
(двусредная ракета или подводный аппарат). При описании движения тела в воде,
помимо остальных сил, нужно учитывать действие гидродинамических реакций и
архимедовых сил. В случае равномерного прямолинейно - поступательного движения
тела в воде, гидродинамические реакции можно определить через аэродинамические
коэффициенты, полученные экспериментально, используя гипотезу стационарности.
При всяком другом движении (с ускорением), приходиться учитывать дополнительные
гидродинамические реакции. Примем следующие допущения: тело движется в
неограниченной, невязкой (идеальной), несжимаемой жидкости. В этом случае
движение жидкости, вызванное движением тела, будет безвихревым (потенциальным).
При таком движении существует потенциал скорости неустановившегося движения
жидкости, функция![]() =
= ![]() (x,y,z,t).
(x,y,z,t).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.