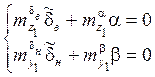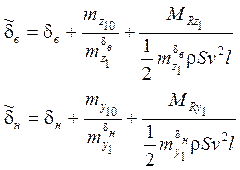
Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения, страница 14

                                                                                                                   (*)

Рассмотрим, как получается одно из балансировочных соотношений:

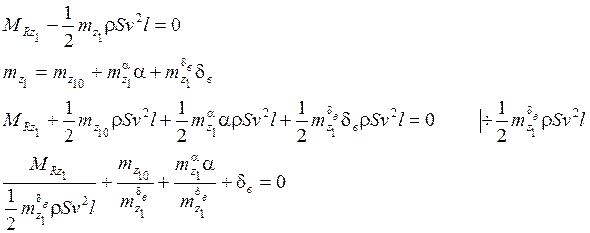
Получим 

Углы  и , определяемые из  соотношения (*), называются балансировочными углами атаки и скольжения , .

Полагаем  малыми величинами; получим из общей системы I с учётом вышеизложенных допущений уравнения пространственного движения ц.м. :

                                                                                       (**)

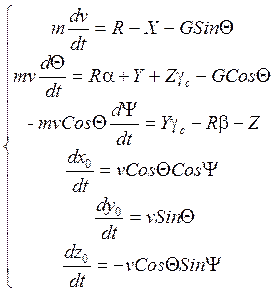Если считать  (крен стабилизирован), то система (**) вместе с системой (*) определяют  при заданных начальных условиях (при этом  считаются известными).

25.03.05

Разделение пространственного движения ЛА

на продольное и боковое.

Система уравнений (I) существенно упрощается, если удается ее разделить на две подсистемы меньшего порядка, чем исходная: систем уравнений продольного движения и систему уравнений бокового движения.

Первая  описывает движение ЛА в вертикальной плоскости.

Вторая  - движение ЛА в горизонтальной плоскости и движение крена.

Принципиальная возможность такого разделения обусловлена наличием симметрии ЛА относительно плоскости x₁y₁. Разделение возможно, если боковое движение обладает малой интенсивностью, т.е. параметры бокового движения γ, γ_с, Ψ, ψ, β, ω_х, ω_у, δ_н, δ_э, z_о являются малыми величинами (произведениями малых величин можно пренебречь по сравнению с самими величинами). Кроме того, предполагается, что коэффициент лобового сопротивления С_х является функцией числа Маха (С_х = С_х (М, α, δ_в)) и не зависит от параметров бокового движения. Это управляемые крылатые и баллистические ракеты.

Неуправляемые НРС, стабилизируемые оперением. Под этот способ упрощения не попадают ЛА, стабилизируемые вращением, у которых угловая скорость ω_х1 – большая величина. Это артиллерийские снаряды, турбореактивные снаряды.

Если указанные 2 условия выполняются, тогда 1-ое, 2-ое, 9-ое, 10-ое, 11-ое уравнения системы (I) не будут содержать указанных параметров бокового движения, т.к. соответствующие члены этих уравнений будут величинами 2-го порядка малости и могут быть отброшены. Помимо этого, как и раньше, можем считать, что sinα ≈ α, cosα ≈ 1. Например, запишем еще раз 2-ое уравнение:

mv(d/dt) = (Rsinα + Y)cosγ_с + (Rcosα sinβ + Z)sinγ_с - Gcos

В соответствии со сказанным, во 2-ом уравнении можно положить, что cosγ_с ≈ 1; sinβ ≈ β; sinγ_с ≈ γ_с; Zsinγ_с ≈ 0; Z ≈ β; R cosα sinβ sinγ_с ≈ Rβγ_с ≈ 0

mv(d/dt) = Rα + Y - Gcos

Аналогично поступаем и с остальными уравнениями движения. Тогда в этом случае уравнения продольного движения запишутся в следующем виде:

m(dv/dt) = R – Gsin - X    (τ)                               движение ц.м.

__

mv(d/dt) = Rα - Gcos + Y        (n)       (II)                     

Jz1(dωz1/dt) = MRZ1 + MAZ1             (относительно Z1)

вращательное движение относительно ц.м.

(d/dt) = ω_z1;   (dx₀/dt) = vcos;  (dy₀/dt) = vsin;

sin≈sin–αcos (это уравнение можно преобразовать к виду ≈-α)

Эту систему обозначим (II)

R = R(y₀)

m = m(t)

J_Z1 = J_Z1(t)

G = mg

X = ½C_xρSv²

Y = ½C_yρSv²

M_AZ1 = ½mρSv²ℓ

C_x = C_x(M, α, δ_в)

C_y = C_y(M, α, δ_в)

C_y = C_y^α · α + C_y^δв · δ_в

m_Z1 = m_Z10 + m_Z1^α · α + m_Z1^δв · δ_в +  · (ω_Z1ℓ/V) + m  · (ℓ/v)

Это система уравнений продольного движения.

В уравнение 2 параметры бокового движения не входят. Это означает, что система (II) может быть решена независимо от остальных уравнений системы (I). Не трудно видеть, что продольное движение может существовать самостоятельно, как движение в данной вертикальной плоскости (плоскости стрельбы), когда не возникает отклонений органов управления рысканьем и креном (δ_н и δ_э) и отклонений боковых параметров движения от их нулевых значений в результате действия ветра. Практически это означает, что указанные возмущения должны достаточно быстро ликвидироваться. Раз оно (движение) может существовать самостоятельно, то уравнение продольного движения можно записать независимо от пространственной системы (I) как уравнение плоско-параллельного движения ЛА в вертикальной плоскости х₀у₀, совпадающей с плоскостью симметрии V,  , ω_Z1,  , α , x₀, y₀, δ_в.