Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения, страница 3

Угол атаки – угол между проекцией скорости ц.м. на плоскость симметрии (линии М₃) и осью ЛА.

При нормальном (правильном) полёте ЛА углы  и  являются малыми углами <15^o

(15^o – критичный угол атаки).

Таблица 3.

	х1	y1	z1
x	с11	с12	с13
y	с21	с22	с23
z	с31	с32	с33

Матрица С тоже является ортогональной, следовательно ;

                 

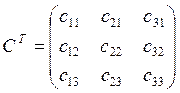
Аналогично можно записать линейные преобразования в матричном виде:

;                  

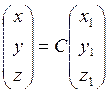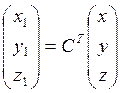
Формулы направляющих косинусов:

,        ,                

Геометрические соотношения.

Устанавливают связь между углами, ориентирующими ЛА в различных системах координат:

Для решения поставленной задачи используем таблицы направляющих косинусов 1, 2 и 3 и соответствующие этим таблицам матрицы.

Таблица 1                              Таблица 2                              Таблица 3

                                                                          (*)

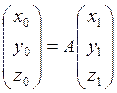
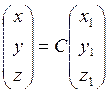А(),   ,    

Поэтому, установив связь между матрицами, можно установить связь между углами. Задача сводится к нахождению связи между матрицами F(A,B,C)=0.

Из (*):    

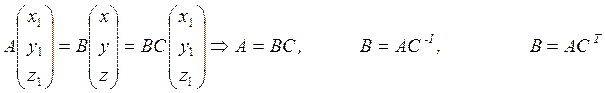
Обращаемся к матрице В и смотрим в какой элемент матрицы В наиболее простым образом входит угол :

 

(2 строку матрицы А умножаем на 1 столбец матрицы , подставляем значения из таблиц 1, 2 и 3)

- малы (крен стабилизирован), тогда

15.02.05 *

3 строку матрицы А умножаем на 1 столбец матрицы :

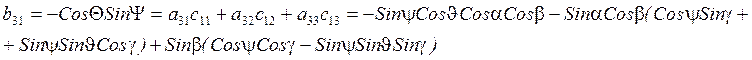
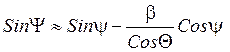
- малы

- малы

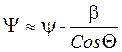
Определяем :

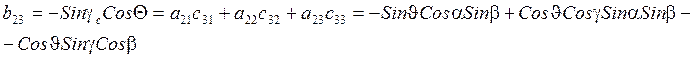
- малы (мал, т.к. крен стабилизирован)

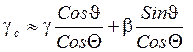
В случае горизонтального полёта ЛА на постоянной высоте

Во внешней баллистике, механике полёта и теории гироскопа встречаются другие углы Резаля:  - угол прецессии,  - угол нутации,  - угол ротации.

Во внешней баллистике используются углы Де-Спарра:

Ориентируют по разному полускоростную и связанную с.к.

 - полускоростная с.к.

 - связанная с.к.

Кинематические соотношения.

Кинематические соотношения служат для определения линейных или угловых координат ЛА в зависимости от линейных или угловых скоростей. При изучении движения ракеты вблизи поверхности Земли со скоростями, меньшими первой космической, можно не учитывать орбитальное движение Земли и её вращательное движение, а поверхность Земли считать плоской. В этом случае стартовую с.к. , где  - точка старта, можно считать инерциальной, т.е. абсолютно неподвижной. При этих условиях выведем основные кинематические соотношения:

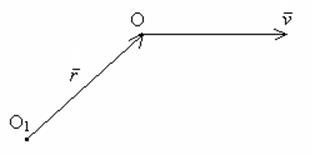
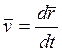 (т.к. точка О₁ неподвижна)                                                                                              (1)

 - координаты ц.м. в стартовой с.к.

 - абсолютная скорость (скорость относительно инерциальной с.к.), путевая скорость

 - орты соответствующих осей стартовой с.к.

Подставляем в уравнение (1):

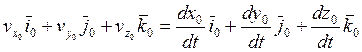
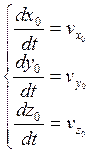                                                                                                                           (2)

(2) – служат для определения ц.м.

Запишем выражения для проекций скорости ц.м.на координатные оси стартовой с.к. Для этого обратимся к рисунку 2 и таблице 2:

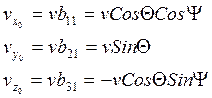
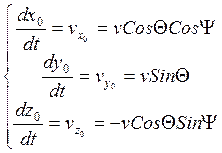
Для определения углов поворота  нужно вывести ещё 3 уравнения. Для их вывода обратимся к рисунку 1:

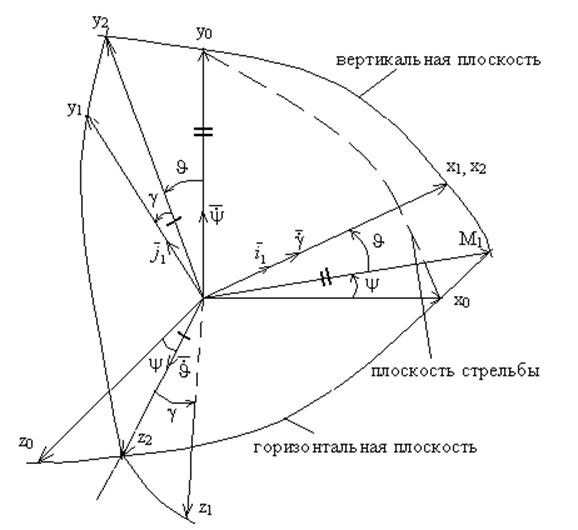
Кроме того воспользуемся соотношением (3):

                                                                                                                      (3)

Спроектируем равенство (3) на оси x₁, y₁, z₁:

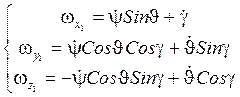                                                                                              (4)

Из (4) найдём :

Домножим второе уравнение на , третье – на , затем их сложим:

Домножим второе уравнение на , третье – на  и вычтем:

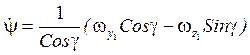
Из первого уравнения системы (4):

Упростим ( - малы):

                                                                                                            

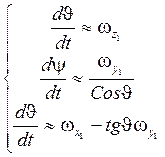
Уравнения динамики.