Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения, страница 25

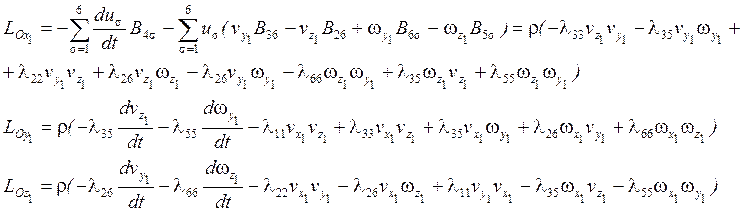
Для управляемой баллистической ракеты  - малые величины

 - угол атаки,   - угол скольжения

 - немалая

Учитывая это, можно записать:

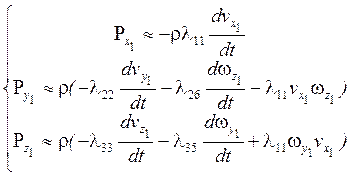                                                                        (14)

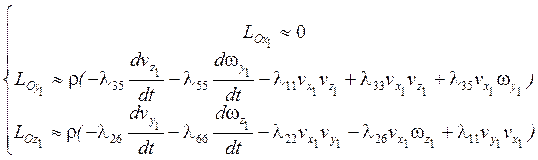                                  (15)

Полученные формулы не учитывают влияние трения и вихреобразование (жидкость идеальная, её движение безвихревое).

29.04.05

Учёт сил трения и вихреобразования.

Учёт этих сил и моментов будем производить следующим образом: записав аэродинамические силы и моменты в форме, принятой в аэродинамике ЛА, и, определив аэродинамические коэффициенты опытным путём (используется гипотеза стационарности), добавим к этим силам и моментам лишь те слагаемые из формул (14) и  (15), которые обусловлены неустановившемся движением тела в жидкости (непозиционные члены), а также слагаемые, которые не учитываются в аэродинамическом эксперименте.

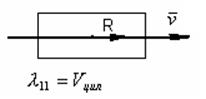
В проекции главного вектора аэродинамических сил на оси связанной системы координат в воздухе.

;

 

X = ½C_xρSv^2;

Y = ½C_yρSv^2;

Z = ½C_zρSv^2;

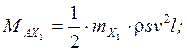
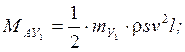
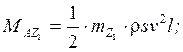
Добавляем в эти формулы из формул (14) и (15), указанные слагаемые:

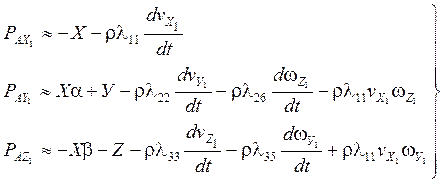                      (16)

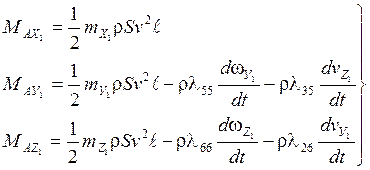                                     (17)

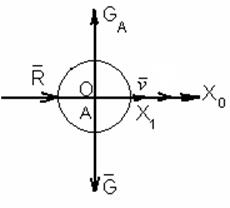
Надо учесть силу Архимеда и момент силы Архимеда:

Сила Архимеда приложена в центре величины ЛА (метацентре – точке А). Метацентр расположен на оси ЛА и, как правило, не совпадает с центром тяжести.

;

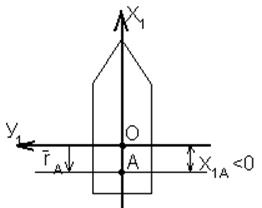 - сила Архимеда;

 - сила тяжести;

;

Обозначим .

Проекцию силы  на оси x1,y1 и z1 найдём, используя таблицу 1 направляющих косинусов.

Используем вторую строчку таблицы 1:

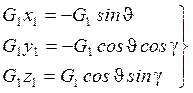                                                                                  (18)

Сила Архимеда даст момент, относительно центра тяжести:

;

 - момент силы ;

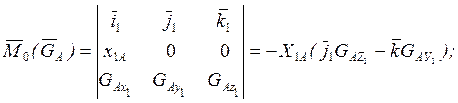
Запишем систему уравнений пространственного движения тела в воде в проекциях на оси связанной системы координат Оx1, y1, z1  при малых значениях α, β,  ω_х1, ω_у1, ω_z1.

Мы знаем такие уравнения динамики:

1) 

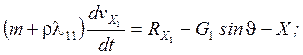
2) 

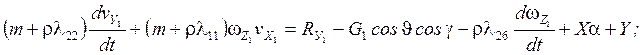
3) 

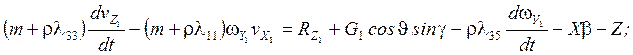
4) 

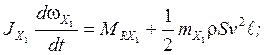
5) 

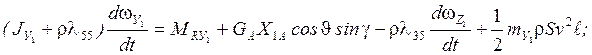
6)  

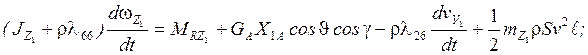
X = ½C_xρSv^2;

Y = ½C_yρSv^2;

Z = ½C_zρSv^2;

  

  ;    

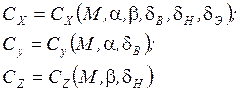
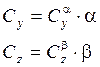
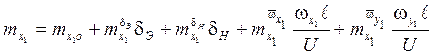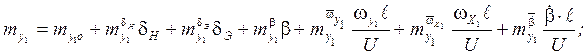
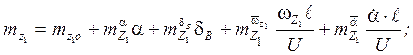
Пример:

                                                                  

    

     

                                                                                                                                                                  

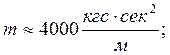
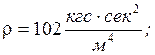
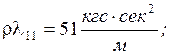
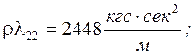
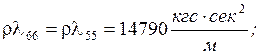
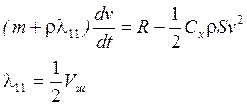
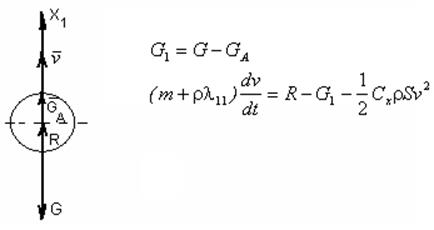
ЛА как звено контура управления. Передаточные функции ЛА.

При построении математической модели динамических систем используются 2 метода:

Первый метод можно условно назвать методом естественных дифференциальных уравнений. Его сущность заключается в построении замкнутой системы дифференциальных уравнений на основе законов физики и механики, обычно выражающихся в дифференциальной форме.

Второй метод можно условно назвать методом типовых звеньев. В соответствии с ним, система представляется в виде совокупности, соответствующим образом соединённых звеньев, для которых дифференциальные уравнения уже имеются.

Этот второй метод наиболее пригоден для анализа стационарных линейных систем на базе операционного исчисления. После того, как динамическая система разделена на ряд типовых звеньев, определяется их передаточная функция.

ПФ системы определяется путём преобразования структурных схем. При изучении динамических свойств ЛА, представим его в виде линейной стационарной модели, то есть опишем его динамику системой линейных дифференциальных уравнений с постоянными коэффициентами. Такая система получается путём линеаризации общей пространственной системы (I) относительно заданного невозмущённого (идеального) движения. При этом, если невозмущённое движение является нестационарным (т.е. переменные параметры), то для приведения линеаризованной системы к стационарному виду используется приём «замораживания» коэффициентов.