А в этой области частот оказываются частоты колебаний жидкого топлива в баках и низкие собственные частоты упругих колебаний корпуса. В результате система управления реагирует не только на угловые колебания корпуса как твёрдого тела, но и на угловые упругие деформации. Таким образом, возникают дополнительные обратные связи, и колебания в системе стабилизации оказываются взаимосвязанными с другими колебаниями. Возникают дополнительные колебания органов управления, благодаря реакции на упругие колебания. Эти отклонения, в свою очередь, вызывают упругие колебания и могут повлиять на устойчивость замкнутой системы стабилизации.
Если частота среза системы стабилизации, и частота упругих колебаний близки друг к другу, то может возникнуть явление резонанса, кроме того, упругие колебания ЛА приводят к дополнительным аэродинамическим нагрузкам (из-за появления местных углов атаки), которые в свою очередь вызывают дополнительные упругие деформации. Это называется явлением Флаттера.
Мы будем рассматривать учёт упругих поперечных
колебаний корпуса. Имеется рекомендация: этот учёт нужно производить, если
длина калибра 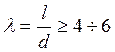 ;
;
Уравнения упругих поперечных колебаний корпуса. Построение решения этого уравнения.
Для изучения поперечных колебаний, корпус ЛА обычно заменяют прямым неоднородным упругим стержнем с незакреплёнными концами (в полёте). При составлении уравнений поперечных колебаний корпуса ЛА, следует учитывать силы внутреннего неупругого сопротивления конструкции и продольные усиления, вызванные тягой двигателя, силой тяжести и движением топлива. Однако, для упрощения задачи, часто принимают допущение, что внутреннее конструкционное демпфирование отсутствует и не учитывает влияние продольных усилий. Тогда дифференциальное уравнение упругих поперечных колебаний корпуса записываются так (смотри рисунок):
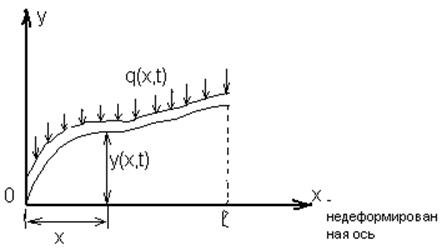
l - длина;
у - отклонение;
На ЛА действует погонная нагрузка q(x,t).
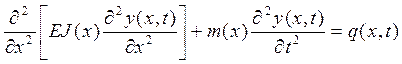 (1)
(1)
Х - координата точки на продольной оси ЛА;
y(x,t) - смещение точки с координатой Х в направлении, перпендикулярном недеформированной оси балки;
Е - модуль упругости (Юнга), характеристические свойства материала;
J(x) - момент инерции площади поперечного сечения балки относительно нейтральной оси сечения, перпендикулярной плоскости колебаний;
EJ(x) - изгибная жёсткость в сечении с координатой х;
m(x) - погонная масса(масса единицы длины);
q(x,t) - погонная внешняя нагрузка, действующая перпендикулярно оси балки;
Значения y(x,t) будут зависеть от начальных значений координат и скоростей точек продольной оси балки от граничных условий на концах балки: y(x,0)
![]() (x,0)
(x,0)
Для корпуса ЛА, оба конца которого свободны, эти граничные условия будут выражать факт равенства нулю перерезывающей силы и изгибающего момента на концах балки. Таким образом, для определения смещения у, надо решить уравнение (1) при граничных условиях (2) и (3), и начальных условиях (*):
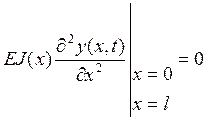 (2)
(2)
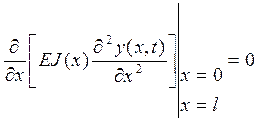 (3)
(3)
Начальные условия:
y(x,0)= ![]() (*)
(*)
![]() (x,0)=
(x,0)= ![]()
Решения уравнения (1), при условиях (2),(3),(*), можно представить в виде суммы (4):
y(x,t)=![]() (4) , где
(4) , где
![]() - функция, выражающая свободное
поперечное колебание;
- функция, выражающая свободное
поперечное колебание;
![]() - функция, выражающая вынужденное
поперечное колебание;
- функция, выражающая вынужденное
поперечное колебание;
Функция ![]() определяется как
решение соответствующего однородного уравнения (q(x,t)=0), удовлетворяющего граничным
условиям (2) и (3), и начальным условиям (*).
определяется как
решение соответствующего однородного уравнения (q(x,t)=0), удовлетворяющего граничным
условиям (2) и (3), и начальным условиям (*).
Функция ![]() определяется как
решение данного неоднородного уравнения (1), удовлетворяющего граничным
условиям (2) и (3), и нулевым начальным условиям.
определяется как
решение данного неоднородного уравнения (1), удовлетворяющего граничным
условиям (2) и (3), и нулевым начальным условиям.
При таком выборе ![]() ,
, ![]() , их сумма будет искомым общим решением
уравнения (1).
, их сумма будет искомым общим решением
уравнения (1).
Определение свободных колебаний.
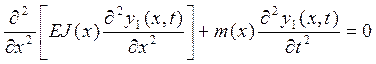 ;
(5)
;
(5)
Надо решить соответствующее однородное уравнение. Общее решение этого уравнения (5) находим, используя метод Фурье, где
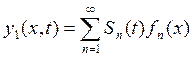 ;
(6)
;
(6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.