Приводятся методы приближённого решения задачи 9+11+12. Наиболее эффективный – метод итерации (последовательных приближений). Его описание можно найти в учебном пособии: Санников В.А., Толпегин О.А. «Динамические свойства ЛА».
Будем считать, что функции ![]() определены каким-либо методом.
определены каким-либо методом.
![]()
Собственные колебания затухают, и основное влияние оказывают вынужденные колебания.
Определение вынужденных поперечных колебаний.
Вынужденные поперечные колебания определяются:
![]()
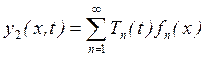 (15)
(15)
![]() - форма свободных колебаний
- форма свободных колебаний
![]() - нормальная координата,
характеризует прогиб по n-ой форме в процессе
вынужденных колебаний.
- нормальная координата,
характеризует прогиб по n-ой форме в процессе
вынужденных колебаний.
Определим ![]() . Для
решения этой задачи нужно подставить предполагаемый вид решения (15) в
уравнение (1).
. Для
решения этой задачи нужно подставить предполагаемый вид решения (15) в
уравнение (1).
![]()
Подставляя предполагаемый вид решения (15) в уравнение (1), получим:
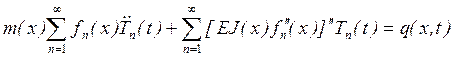
Т.к. ![]() удовлетворяет уравнению
(7), то из этого уравнения можно записать:
удовлетворяет уравнению
(7), то из этого уравнения можно записать:
![]()
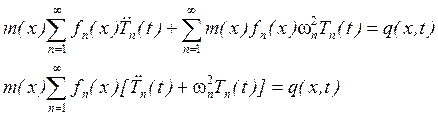
Умножим левую и правую части уравнения на ![]() и проинтегрируем от 0 до l. Воспользуемся свойством ортогональности (14).
Получаем:
и проинтегрируем от 0 до l. Воспользуемся свойством ортогональности (14).
Получаем:
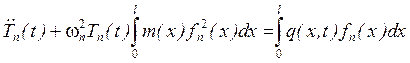
Обозначим:
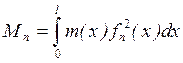
Тогда для определения нормальной координаты будем иметь следующее уравнение:
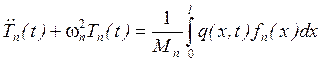 (16)
(16)
(16) – линейное неоднородное уравнение 2 порядка с постоянным коэффициентом
Это уравнение должно решаться при следующих начальных условиях:
![]()
Общий вид решения уравнения (16):
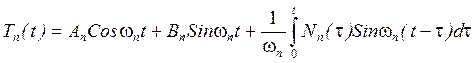 (17)
(17)
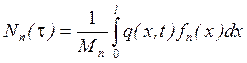
Т.к. начальные условия нулевые ![]() , то
, то ![]()
![]() - произвольные постоянные
- произвольные постоянные
Окончательно получаем:
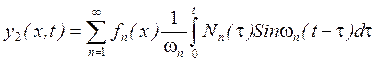 (18)
(18)
Обычно на практике имеют значение только 2
первые формы ![]() .
.
Определение погонной поперечной нагрузки.
На ЛА в полёте могут действовать распределённые и сосредоточенные силы. Тягу будем считать сосредоточенной силой, подъёмную силу отклонения руля – сосредоточенной силой, аэродинамическую силу – распределённой. При этом при определении погонной нагрузки обычно пренебрегают составляющей силы тяжести в направлении, перпендикулярном продольной оси ракеты. Не учитывают дополнительных аэродинамических сил, вызванных упругими колебаниями. В этом случае влияние упругих колебаний проявляются лишь в том, что вектор тяги получает дополнительное угловое отклонение, равное углу наклона упругой линии в точке приложения тяги, а сама точка приложения смещается от центральной оси жёсткого ЛА на величину прогиба.
Запишем выражение для погонной нагрузки.
Рассмотрим общие положения.
Пусть на балку кроме распределённой нагрузки действует сосредоточенная сила на расстоянии xr , сосредоточенный момент.
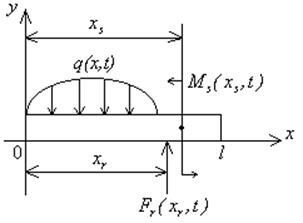
Запишем выражение для погонной нагрузки от этих
сосредоточенных силовых факторов. Оказывается, сосредоточенные силу и момент
можно распределить по длине балки (т.е. заменить погонной нагрузкой) с
использованием ![]() -функции Дирака.
-функции Дирака.
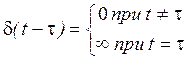
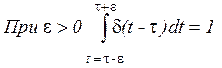
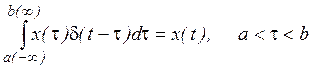
![]() -функция «съедает» интеграл
-функция «съедает» интеграл
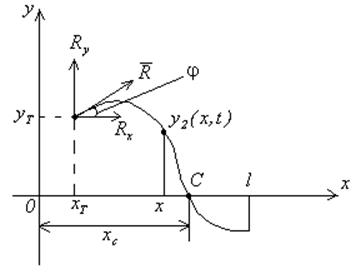
![]() - недеформированная ось
- недеформированная ось
![]() - угол поворота сечения
деформированного корпуса относительно оси z
- угол поворота сечения
деформированного корпуса относительно оси z
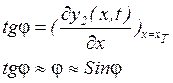
![]()
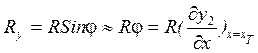
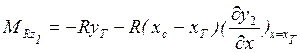
Погонная нагрузка от тяги:
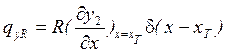
Погонная нагрузка от аэродинамических сил:
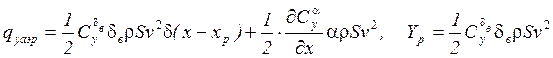
![]() - центр давления руля высоты
- центр давления руля высоты
![]() - погонное значение коэффициента
- погонное значение коэффициента
![]()
Суммарная погонная нагрузка:
![]()
15.04.05
![]()
![]() ;
;
Пренебрежение погонной нагрузкой от тяги означает, что мы не учитываем взаимного влияния вынужденных колебаний по одной форме, на вынужденные колебания по другой форме. Следовательно, мы можем записать следующее выражение для погонной нагрузки:
![]() , где
, где
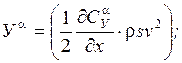
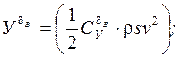
Можно считать, что погонное
значение 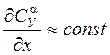 , тогда можно записать, что:
, тогда можно записать, что:
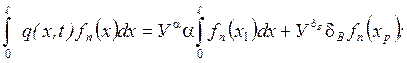
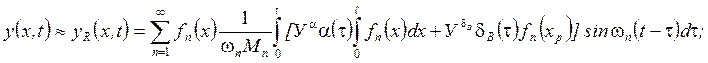
Уравнение продольного движения с учётом упругих поперечных колебаний корпуса.
При записи уравнений движения центра масс будем использовать связанную систему координат. В связанной системе координат ускорение центра масс равно:
![]()
![]() ;
;
![]() ;
;
Первое уравнение на ![]() : m(dv
: m(dv![]() /dt) = R – Gsin
/dt) = R – Gsin![]() - Xсоs
- Xсоs![]() +Ysin
+Ysin![]() ;
;
Второе уравнение на ![]() :
: 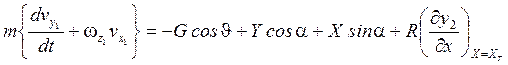 ;
;
Третье уравнение на ![]() :
: 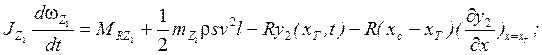
Четвёртое уравнение - кинематическое: 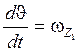 ;
;
Пятое уравнение: ![]() ;
;
Шестое уравнение - определение координаты: 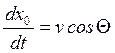 ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.