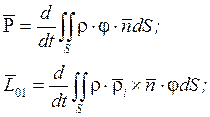
![]()
Преобразуем формулы (8) и (9). Введём следующие обозначения:
обозначим вектор 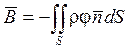 -
импульсивная сила;
-
импульсивная сила;
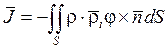 - импульсивная пара;
- импульсивная пара;
Тогда формулы (8), (9) можно переписать так:
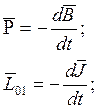
![]()
Нас интересует момент гидродинамический не
относительно неподвижной точки ![]() , а относительно центра
тяжести через
, а относительно центра
тяжести через ![]() и
и![]() , он
определяется по формуле (10):
, он
определяется по формуле (10):
![]() (10)
(10)
Подставляя в формулы ![]() и
и ![]() значения
значения ![]() и
и ![]() после ряда преобразований, окончательно
получим следующие выражения для гидродинамических реакций
после ряда преобразований, окончательно
получим следующие выражения для гидродинамических реакций ![]() и
и ![]() :
:
26.04.05 *
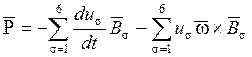 (11)
(11)
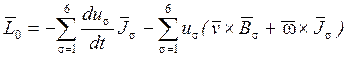 (12)
(12)
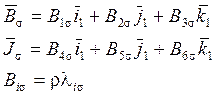
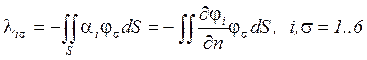 (13)
(13)
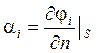
![]() - коэффициенты присоединённых
масс
- коэффициенты присоединённых
масс
Т.о. определение гидродинамических реакций сводится к определению коэффициентов присоединённых масс.
Векторные уравнения движения тела в воде.
Обозначим:
![]() - вектор количества движения
тела
- вектор количества движения
тела
![]() - момент количества движения
тела (кинетический момент относительно
- момент количества движения
тела (кинетический момент относительно ![]() )
)
![]() - главный вектор внешних сил,
действующих на тело помимо гидродинамических реакций
- главный вектор внешних сил,
действующих на тело помимо гидродинамических реакций
![]() - главный момент внешних сил
помимо гидродинамических моментов
- главный момент внешних сил
помимо гидродинамических моментов
Тогда по теоремам механики можно записать:
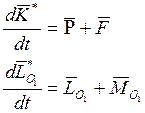
Подставляем в эти уравнения значения ![]() и
и
![]() из (8) и (9):
из (8) и (9):
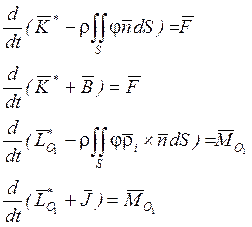
Сравним эти уравнения с теми, которые получатся, если тело движется в пустоте. Если тело движется в пустоте, то гидродинамические реакции отсутствуют:
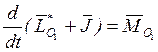
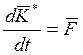
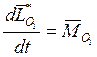
Движение тела в жидкости происходит так, будто к
главному вектору количества движения ![]() присоединилось
добавочное количество движения
присоединилось
добавочное количество движения ![]() , а к главному моменту
количества движения присоединился добавочный момент количества движения
, а к главному моменту
количества движения присоединился добавочный момент количества движения ![]() . Поэтому векторы
. Поэтому векторы ![]() и
и
![]() получили название присоединённых количества
движения и момента количества движения. Они выражаются через коэффициенты
присоединённых масс.
получили название присоединённых количества
движения и момента количества движения. Они выражаются через коэффициенты
присоединённых масс.
Коэффициенты присоединённых масс.
Всего их 36. Эти коэффициенты определяются
формулой (13) и зависят только от формы тела и выбора с.к.. Однако, как
доказывается в теории, матрица этих коэффициентов симметрична: ![]() . Т.о. для произвольной формы тела разных
коэффициентов будет 21. Для симметричных тел с определённой степенью симметрии
часть из 21 коэффициента обращается в нуль. Так, например, если тело имеет одну
плоскость симметрии (
. Т.о. для произвольной формы тела разных
коэффициентов будет 21. Для симметричных тел с определённой степенью симметрии
часть из 21 коэффициента обращается в нуль. Так, например, если тело имеет одну
плоскость симметрии (![]() ), то отличны от нуля 12
коэффициентов, а остальные 9 равны нулю.
), то отличны от нуля 12
коэффициентов, а остальные 9 равны нулю.
плоскость симметрии ![]()
|
Равны нулю |
Отличны от нуля |
|
|
|
Если 2 плоскости симметрии, то отличны от нуля 8
коэффициентов, а остальные 13 равны нулю. Если тело имеет 3 плоскости
симметрии, то отличны от нуля 6 коэффициентов: ![]() , а
остальные равны нулю.
, а
остальные равны нулю.
Если тело вращения и ![]() - ось
вращения, то коэффициент
- ось
вращения, то коэффициент ![]() =0, т.к. вращательное
движение этого тела относительно оси
=0, т.к. вращательное
движение этого тела относительно оси ![]() не вызывает возмущения
жидкости. Можно сказать, что для тела вращения (например, баллистической
ракеты) отличны от нуля следующие 7 коэффициентов:
не вызывает возмущения
жидкости. Можно сказать, что для тела вращения (например, баллистической
ракеты) отличны от нуля следующие 7 коэффициентов: ![]() , при
этом
, при
этом ![]() ,
, ![]() ,
, ![]() . Т.о. в этом случае для тела вращения с
осью
. Т.о. в этом случае для тела вращения с
осью ![]() достаточно определить только 4 разных
коэффициента присоединённых масс.
достаточно определить только 4 разных
коэффициента присоединённых масс.
Теоретические формулы определены для
ограниченного класса тел. Характерный пример – эллипсоид. Для эллипсоида с
осями ![]() они приведены в учебном пособии В.А.
Санников, А.С. Шалыгин «Математические модели динамики полёта ЛА».
они приведены в учебном пособии В.А.
Санников, А.С. Шалыгин «Математические модели динамики полёта ЛА».
Для шара 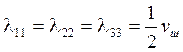 ,
, ![]() - объём шара, а остальные коэффициенты
равны нулю.
- объём шара, а остальные коэффициенты
равны нулю.
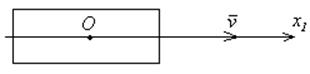
Для цилиндра, который двигается в направлении
своей оси ![]() .
.
Для тел более сложной формы результаты не получены.
Для тел произвольной формы советскими учёными И.С. Риманом и Р.А. Крепс разработан метод колебаний.
Выражение для проекций гидродинамических сил и моментов на оси связанной с.к. Ox1y1z1 в случае пространственного движения баллистической ракеты в воде.
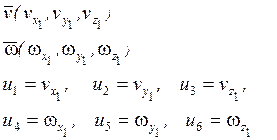
![]()
![]() :
: ![]()
![]()
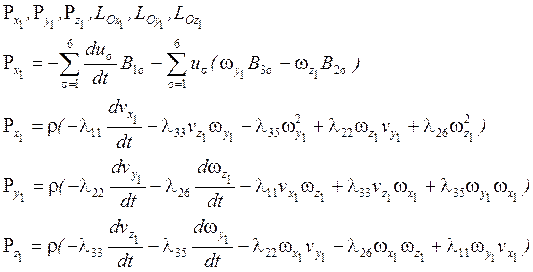
Для проекций гидродинамического момента:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.