Найдём ![]() , вызванное отклонением
руля высоты на постоянный угол:
, вызванное отклонением
руля высоты на постоянный угол:
![]() (используем предельную теорему
преобразования Лапласа)
(используем предельную теорему
преобразования Лапласа)
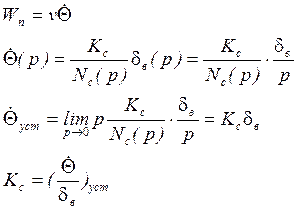
Т.о. коэффициент усиления ЛА ![]() характеризует
маневринность ЛА: чем больше
характеризует
маневринность ЛА: чем больше ![]() , тем больше при
постоянном
, тем больше при
постоянном ![]() угловая скорость касательной к траектории,
т.е. маневренность.
угловая скорость касательной к траектории,
т.е. маневренность.
Рассмотрим физический смысл скоростной
постоянной времени ![]() . Для этого используем ПФ:
. Для этого используем ПФ:
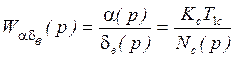
Найдём установившееся значение ![]() при
при ![]() :
:
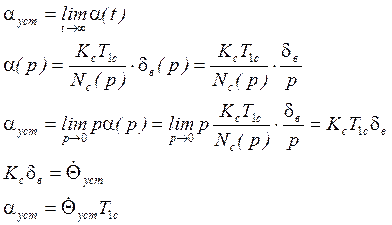
Отсюда можем записать:
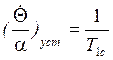
Из последнего выражения следует, что чем больше ![]() , тем больший угол
, тем больший угол ![]() требуется
для создания нужной величины
требуется
для создания нужной величины ![]() при данном отклонении
руля высоты. Т.о. при увеличении
при данном отклонении
руля высоты. Т.о. при увеличении ![]() ЛА становится более
инерционным по отношению к стремлению внешних сил изменить направление его
движения.
ЛА становится более
инерционным по отношению к стремлению внешних сил изменить направление его
движения.
Найдём закон изменения ![]() при
изменении угла тангажа
при
изменении угла тангажа ![]() на постоянное значение.
на постоянное значение.
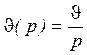
Для решения этой задачи воспользуемся ПФ:
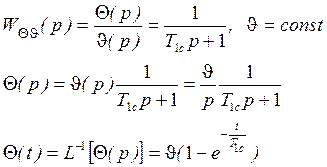
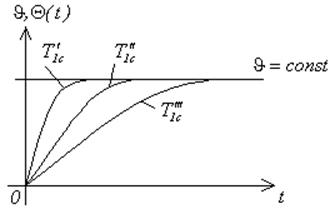
![]()
Чем больше ![]() , тем больше времени
требуется для изменения направления движения
, тем больше времени
требуется для изменения направления движения ![]() .
.
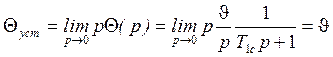
![]() - постоянная времени ЛА
- постоянная времени ЛА
![]() - коэффициент демпфирования
- коэффициент демпфирования
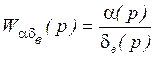
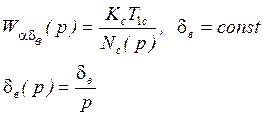
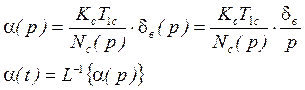
Для реальных ЛА ![]() .
.
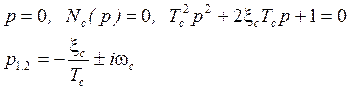
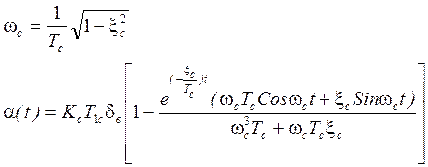
Из последнего выражения следует, что ![]() определяет
величину перерегулирования
определяет
величину перерегулирования ![]() . Чем больше
. Чем больше ![]() , тем меньше перерегулирование и тем
быстрее затухает процесс
, тем меньше перерегулирование и тем
быстрее затухает процесс ![]() . Величина
. Величина ![]() является декриментом затухания процесса
является декриментом затухания процесса ![]() .
.
Постоянная времени ![]() пропорциональна
периоду свободных колебаний и обратно пропорциональна их частоте.
пропорциональна
периоду свободных колебаний и обратно пропорциональна их частоте.
![]() - частота свободных колебаний
- частота свободных колебаний
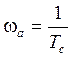 - собственная круговая частота
свободных колебаний
- собственная круговая частота
свободных колебаний
Установим связь параметров ![]() с
аэродинамическими и инерционными характеристиками ЛА. Для этого обратимся к выражениям
для параметров через динамические коэффициенты
с
аэродинамическими и инерционными характеристиками ЛА. Для этого обратимся к выражениям
для параметров через динамические коэффициенты ![]() .
.
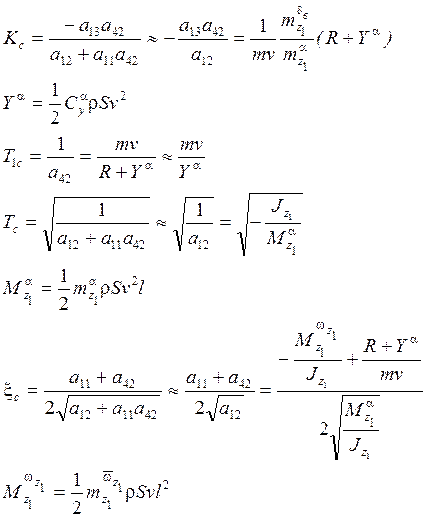
Из этих формул следует, что коэффициент ![]() увеличивается с ростом v и уменьшается с ростом
увеличивается с ростом v и уменьшается с ростом ![]() ,
, 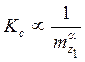 (увеличивая
статическую устойчивость, уменьшаем
(увеличивая
статическую устойчивость, уменьшаем ![]() ).
).
Величина ![]() почти
не зависит от v, но убывает с ростом высоты
почти
не зависит от v, но убывает с ростом высоты ![]() (
(![]() -
плотность воздуха). Т.о. собственное демфирование ЛА при подъёме на высоту
может оказаться недостаточным для получения переходного процесса с заданным
затуханием. Требуемое значение
-
плотность воздуха). Т.о. собственное демфирование ЛА при подъёме на высоту
может оказаться недостаточным для получения переходного процесса с заданным
затуханием. Требуемое значение ![]() , обеспечивающее
заданное качество переходного процесса угловой стабилизации ЛА достигается
выбором параметров контура системы угловой стабилизации.
, обеспечивающее
заданное качество переходного процесса угловой стабилизации ЛА достигается
выбором параметров контура системы угловой стабилизации.
Скоростная постоянная времени 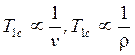 , т.е. с увеличением высоты
, т.е. с увеличением высоты ![]() резко увеличивается, т.е. инерционность
возрастает.
резко увеличивается, т.е. инерционность
возрастает.
Собственная частота 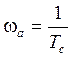 увеличивается
с ростом скорости, а с ростом высоты уменьшается (
увеличивается
с ростом скорости, а с ростом высоты уменьшается (![]() ).
).
20.05.05
Передаточная функция ЛА для бокового возмущённого движения.
Для простоты будем рассматривать осесимметричный ЛА с осью симметрии х1. В этом случае уравнение бокового движения в вариациях запишутся более просто, чем для ЛА самолётной схемы, у которых наблюдается сильное взаимодействие движений рысканья и крена.
У осесимметричных ЛА влияние движения крена на движение рысканья (перекрёстная аэродинамическая связь) не велико и его можно не учитывать. Таким образом, в системе бокового движения в вариациях можно положить нулю динамический коэффициент в10=0, тогда из уравнений бокового движения можно выделить следующую независимую группу уравнений, описывающую короткопериодическое движение рысканья.
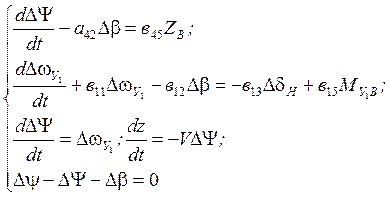 (3)
(3)
Уравнения (3) не отличаются от уравнений (1) продольного
движения в вариациях. Их можно получить из уравнений (1), заменив коэффициенты ![]() , причём
, причём ![]()
![]()
При этом совпадают не только форма уравнений, но и
числовые значения динамических коэффициентов, так как в динамически
осесимметричных ЛА ![]() и т.д. В силу этого совпадения
ПФ для параметров движения рысканья будут иметь такой же вид, как и для
параметров продольного движения.
и т.д. В силу этого совпадения
ПФ для параметров движения рысканья будут иметь такой же вид, как и для
параметров продольного движения.
Таким образом, можно записать следующие выражения для упрощённых ПФ параметров движения рысканья:
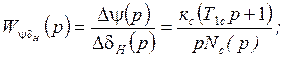
![]() =
=![]() ;
;
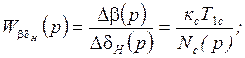
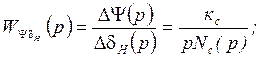
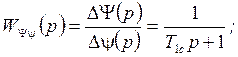
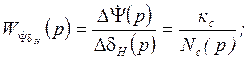
Причём параметры ![]() , Т1с, Тс и
, Т1с, Тс и ![]() определяются по тем же формулам, что и
для продольного движения с заменой
определяются по тем же формулам, что и
для продольного движения с заменой ![]() .
.
Движение крена существенно зависит от движения рысканья, даже для осесимметричной схемы. Выпишем из системы уравнений бокового движения в вариациях уравнения движения крена.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.