Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения, страница 2

Угловая ориентация связанной и стартовой с.к. при совмещённых началах определяется 3 углами (Эйлеровыми углами):

 - угол тангажа

 - угол рысканья

 - угол крена

Связанную и стартовую с.к. можно совместить при помощи 3 поворотов.

Рисунок 1.

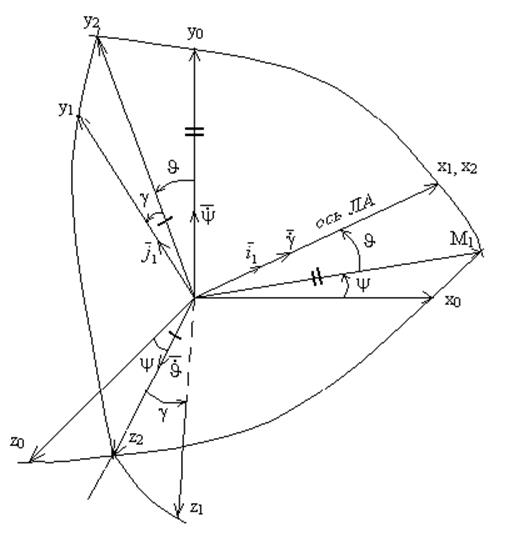
Первый поворот производиться относительно любой оси исходной с.к.

Будем производить первый поворот относительно y₀ на угол  с угловой скоростью .

Второй поворот производится относительно любой из двух осей, вновь образовавшихся в результате первого поворота.

Будем производить поворот относительно оси z₂ на угол  с угловой скоростью .

Третий поворот - относительно оси, занявшей окончательное положение (относительно х₁ на угол ).

                                                       

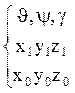
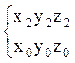
                    Т.к. связанная с.к. со стартовой совмещается с помощью трёх поворотов, а ЛА неизменно связан со связанной с.к., то абсолютная угловая скорость вращения ЛА:

                          (1)

Одновременно  - угловая скорость вращения связанной с.к.

Таблица 1 направляющих косинусов.

	х1	y1	z1
x0	a11	a12	a13
y0	a21	a22	a23
z0	a31	a32	a33

A – ортогональная квадратная матрица, А()

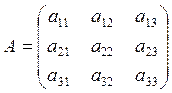
11.02.05 *

 (ортогональная матрица)

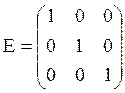
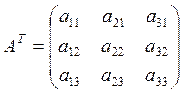
Направляющие косинусы – косинусы между двумя соответствующими направлениями.

Имея таблицу направляющих косинусов, можно записать линейные преобразования в другие при совмещённых началах, а именно:

x₀=а₁₁x₁+a₁₂y₁+a₁₃z₁

y₀=a₂₁x₁+a₂₂y₁+a₂₃z₁

z₀=a₃₁x₁+a₃₂y₁+a₃₃z₁

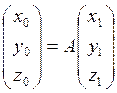
Число столбцов в первой матрице равно числу строк второй матрицы.

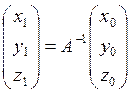
Определение направляющих косинусов (общее правило).

Чтобы найти направляющий косинус между двумя данными направлениями, нужно единичный вектор (орт) одного направления спроектировать на другое. Если угол между двумя данными направлениями не обозначен, то предварительно орт исходного направления раскладывается на компоненты по двум взаимно перпендикулярным направлениям, и каждая компонента затем проектируется на второе направление (если и её нельзя спроектировать, то и её раскладывают на компоненты и т.д.).

Найдём направляющие косинусы (проиллюстрируем правило):

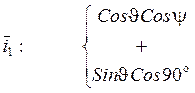
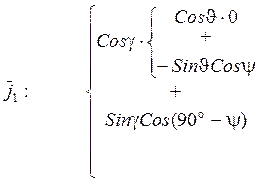
Остальные вывести самостоятельно!

Правило проверки: направляющие косинусы удовлетворяют условиям совместимости и ортогональности. Условие совместимости означает, что сумма квадратов косинусов строки (столбца) равна единице.

Например:

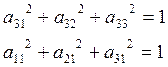
Условие ортогональности означает, что сумма попарных произведений одной строки (столбца) на элементы другой строки (столбца) равна нулю.

Например:

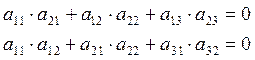
2. Взаимное расположение стартовой, скоростной и полускоростной с.к. при совмещённых началах.

Расположение скоростной и стартовой с.к. при совмещённых началах определяется 3 углами:

 - угол возвышения (угол наклона траектории),  - угол курса

 - скоростной угол крена

Скоростную с.к. можно совместить со стартовой с помощью 3 поворотов

( как в случае рисунка 1).

Рисунок 2.

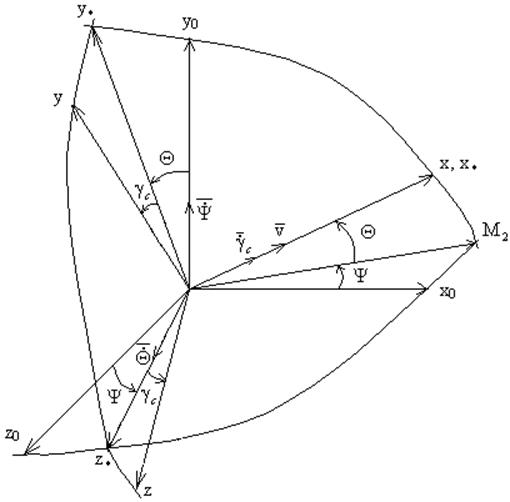
Порядок поворотов:

 

 - угловая скорость скоростной с.к.

 - угловая скорость полускоростной с.к.

Таблица 2.

	х	y	z
x0	b11	b12	b13
y0	b21	b22	b23
z0	b31	b32	b33

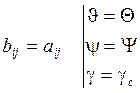
,       и т.д.

Матрица B тоже является ортогональной, следовательно ;

                    

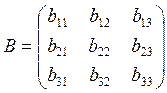
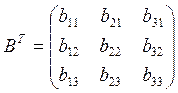
Аналогично можно записать линейные преобразования в матричном виде:

;                  

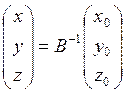
            3. Взаимное расположение связанной и скоростной с.к.

Определяется 2 углами:

 - угол атаки,  - угол скольжения

Следовательно эти системы можно совместить с помощью 2 поворотов.

Рисунок 3.

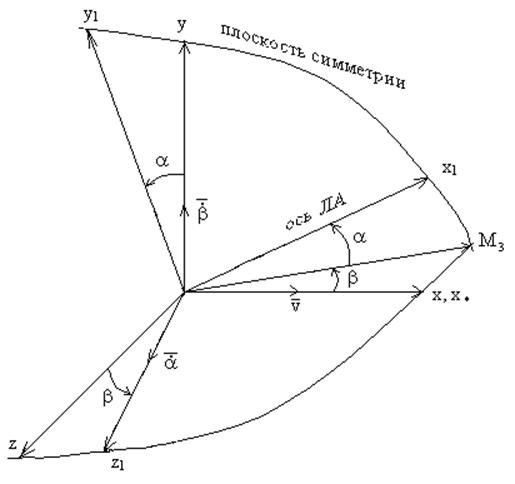
Угол скольжения – угол между вектором скорости  и плоскостью симметрии.