Машиностроение \ Механика полета

Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения, страница 21

Седьмое уравнение: ;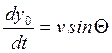

Восьмое уравнение:;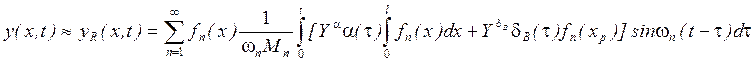

X = ½CxρSv2

Y = ½CyρSv2

Cy = Cyα · α ;

cos ≈ 1; sin ≈ ; Ysin≈;

mZ1 = mZ10 + mZ1α · α + mZ1δв · δв +  · (ωZ1ℓ/v) + m  · (ℓ/v);

δв - известно из уравнения управления.

Учёт влияния колебаний жидкостей в баках в уравнениях движения ЛА. Механический аналог колебаний жидкостей в баках.

Исследование движения твёрдого тела с полостями, частично заполненных жидкостью, является одной из классических проблем механики деформируемых систем. Решение этой проблемы началось с работ Николая Егоровича Жуковского. В последние годы эта проблема стала особенно актуальной для инженерной практики в связи с быстрым развитием и совершенствованием объектов авиационной и ракетной техники. Об этом свидетельствует присуждение в конце 80-ых годов группе учёных, возглавляемой академиками А.Ю. Ишлинским, Н.Н. Моисеевым, А.С. Алексеевым, государственной премии за решение задач учёта колебаний жидкости в уравнениях движения. При решении практических задач динамики объекта с жидким наполнением представляет интерес выявления как движения самой жидкости в полостях, так и возникающих при этом сил, действующих на корпус ЛА со стороны колеблющейся жидкости. Не менее важным является изучение влияния дополнительных степеней свободы, которыми обладают жидкости, на устойчивость невозмущённого движения ЛА. Исключение дополнительных степеней свободы жидкости, далеко не всегда идёт в запас устойчивости, поэтому, например, объект устойчивый по расчётам без учёта подвижности жидкости, в действительности может оказаться неустойчивым. Задача усложняется ещё и тем, что собственное демпфирование колебаний жидкого топлива в больших ракетах слишком мало, так как обратно пропорционально диаметру бака. Учёт дополнительных степеней свободы жидкостей сводится к решению достаточно сложной краевой задачи математической физики (задача Неймана). При решении этой задачи жидкость принимается идеальной (не учитывается трение) и несжимаемой, а её движение - неустановившемся безвихревым. Колебания, перемещения и скорости частиц в жидкости считаются малыми.

Поясним допущение о неучёте сжимаемости: акустическая скорость звука С0=1000 м/с в жидкости на основании эксперимента частоты колебаний жидкости в баках

ж=0.5 - 3  (1/сек.), амплитуда а=(0.01 - 0.1)r0, где r0 - радиус свободной поверхности жидкости в баках. Если считать, что  r0=1м, ж=1 (1/сек), а=0.1 м, то число Маха

М=v/ С0= ж*a/ С0≈.

Считая, что движение безвихревое, которое зависит от:

(x,y,z,t) - потенциал скорости неустановившегося движения жидкости.

При этих допущениях справедлив, для неустановившегося безвихревого движения жидкости, интеграл Лагранжа, который определяет давление в любой точке жидкости:

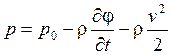, где

 - массовая плотность жидкости;

v - скорость движения частиц жидкости;

- давление жидкости на , где v=0;

р - давление в любой точке жидкости;

;

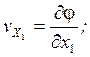
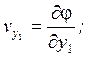
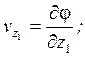
Потенциал скорости  удовлетворяет уравнению Лапласа =0, где

 - оператор Лапласа:

;

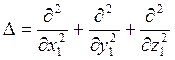Предположение малости отклонений свободной поверхности жидкости от невозмущённого состояния. Для этого потенциала   составляется уравнение в частных производных (уравнение Лапласа). Исследование этого уравнения совместно с системой обыкновенных дифференциальных уравнений, описывающих движение корпуса ЛА, сопряжено с большими трудностями и может быть доведено до конца только для некоторых простейших форм бака: сфера, цилиндр. Получаемые при этом алгоритмы достаточно сложны и для их реализации, как правило, требуется мощное компьютерное обеспечение. Боле простое решение задачи, имеющее точность, достаточную для технических расчётов, может быть получено, если использовать механические модели колебания жидкости в баках. Принцип построения этих моделей основан на определённой аналогии между колебаниями жидкости более массовых сил и колебаниями механических моделей. Параметры модели выбираются такими, чтобы силы и моменты, действующие со стороны моделей на бак при его малых колебаниях, совпадали с аналогичными воздействиями со стороны жидкости. Наиболее широкое распространение получили маятниковые и пружинно-массовые модели колебаний жидкости в баках. Структура и параметры механической модели зависят от формы бака  свойств жидкости. При математическом описании колебаний жидкости путём решения задачи Неймана для уравнения Лапласа, волновой процесс, возникающий на его свободной поверхности, представляется в виде суперпозиции бесчисленного множества тонов колебаний. Каждому тону должна соответствовать своя механическая модель, однако вследствие незначительного влияния по сравнению с первым тоном, высшими тонами колебаний обычно пренебрегают. Это объясняется тем, что масса жидкости, участвующая в колебаниях, уменьшается с увеличением тона. Для цилиндрического бака, равновесное состояние которого характеризуется перпендикулярностью свободной поверхности  жидкости к продольной оси бака, механические модели первого тона колебаний, получающиеся при плоском движении бака, представлены на следующем рисунке.

Скачать файл