Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения, страница 23

Если существует потенциал скорости, то скорость определяется как:

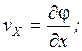
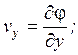
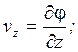
v - скорость частиц жидкости;

А также справедливо соотношение:

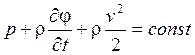; (интеграл Лагранжа)

 - массовая плотность жидкости;

р - давление в жидкости;

Интеграл Лагранжа существует в случае потенциального неустановившегося движения жидкости. Потенциальная функция определяется решением краевой задачи Неймана. Надо решить уравнение Лапласа

=0                                       (1), где

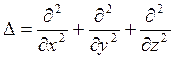 - оператор Лапласа, при следующих граничных условиях:

скорость жидкости в направлении нормали к поверхности тела S равняется проекции скорости тела в направлении нормали к поверхности тела S.

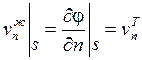                              (2)

- нормаль к поверхности тела S.

Обычно используется связанная с телом система координат.

Преобразуем условие (2):

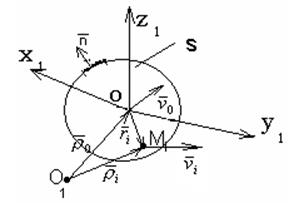
О - центр масс тела;

 - скорость центра масс;

О1 - неподвижная точка пространства;

 - абсолютная угловая скорость вращения тела;

 - скорость точки Мi на поверхности тела S;

S - поверхность;

;

;

;

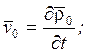
Тогда проекция на нормаль произвольной точки Мi равняется:

Обозначим;

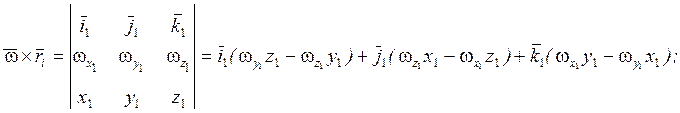
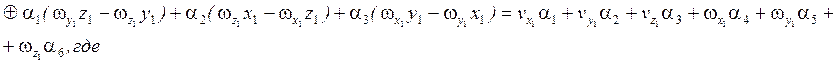
Таким образом 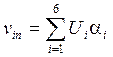, где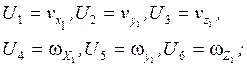

Таким образом, граничное условие (2) можно переписать следующим образом:

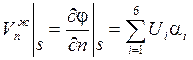;                   (3)

(x1,y1,z1,t), надо решить задачу Неймана (1), при граничных условиях (3).

Особенностью поставленной задачи Неймана является то, что  является функцией времени и координат. Так как время входит в , то в силу граничных условий (3) естественно разыскивать решение задачи (1)+(3) в виде суммы:

                     (x1,y1,z1,t)= 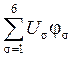;                     (4), причём

=(x1,y1,z1).

Функция  определяется только формой поверхности S и выбором системы координат x1,y1,z1.

Подстановка предполагаемого решения (4) в уравнения (1) и (3) позволяет установить, что функция  удовлетворяет уравнению Лапласа:

                  =0                                (5)

при граничных условиях: 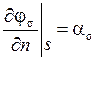             ,         (6)    - задача Неймана для                   функции (x1,y1,z1);

Физический смысл () на основании представления (4).

Из выражения (4) мы можем получить, что    (x1,y1,z1,t)= , если =1, а остальные . Таким образом можно сказать, что соответствует поступательному движению тела в жидкости, параллельно оси с единичной скоростью. Иначе говоря,  - потенциал скорости такого движения жидкости, которое возникает при поступательном движении тела вдоль оси  с единичной скоростью. Аналогичный смысл имеют  и , размерность(i=1,2,3)[м]. Функция [м] соответствует такому движению жидкости, которое возникает при вращении тела около оси  с угловой скоростью =1,  остальные

Функции  и  имеют аналогичный смысл.

 - относительно .

Задача Неймана (5)+(6) имеет точное решение для некоторых простейших форм тела, например, для шара с радиусом в,  очевидно = ==0 (так как трения нет, и жидкость будет неподвижна (идеальна)), а

         

         

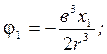
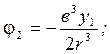
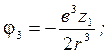
x1,y1,z1 - координаты любой точки жидкости.

Таким образом, мы определим потенциал скорости в случае неустойчивого движения жидкости, которое возникает от движения тела в воде с ускорением.

Расчёт гидродинамических реакций.

Обозначим р - давление в любой точке жидкости.

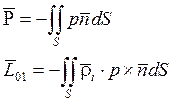                                                  (7)            

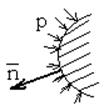
 - момент, относительно неподвижной точки ;                

pdS - элементарная сила;

- радиус - вектор;

Обозначим - давление на , где =0 и U=0, тогда .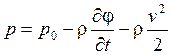

В силу переменности давления р, вычисление интегралов, входящих в (7), затруднительно, поэтому вектора и определяют иным путём - косвенно. Применяя к массе жидкости, заключённой между поверхностью тела S и поверхностью сферы бесконечно большого радиуса, охватывающего рассматриваемое тело, законы количества движения  и моментов количества движения.

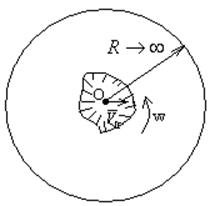
В результате применения законов количества движения и моментов количества движения, мы получаем выражения для гидродинамических реакций: