Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения, страница 13

Анализ этой системы. Методы упрощения.

Запишем полную систему уравнений пространственного движения при закреплённых рулях (мы считаем, что закон отклонения рулей является известной функцией параметров движения).

При записи всех уравнений не будем пренебрегать малыми второго порядка малости относительно параметров движения.

Система I.

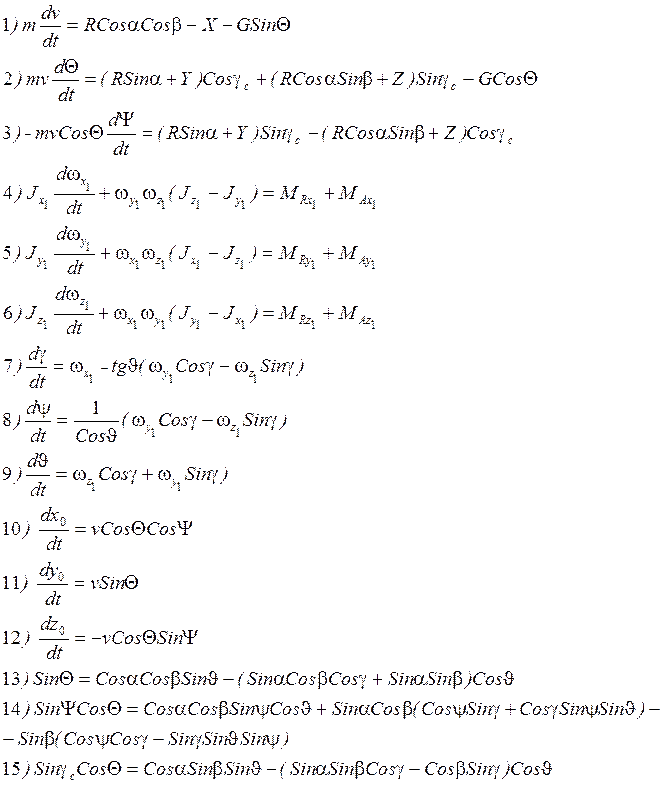
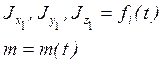
Если закон изменения массы не известен, то к указанной системе добавляем уравнение:

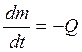, где

Q [кг/сек] – секундный массовый расход; зависит от типа двигателя, режима его работы, скорости и высоты полёта ЛА. Для ракетных двигателей Q можно считать известной функцией времени и в частном случае Q=const.

Интегрируя последнее уравнение, получаем:

m=m₀ – Qt, где m₀ – начальная масса ЛА

R=R(Y₀), 

 - даны в предыдущем изложении

 - эти переменные считаются известными функциями и в частном случае это постоянные величины

Система включает следующие уравнения:

1-3 – уравнения поступательного движения ЛА в проекциях на полускоростные оси

4-6 – уравнения динамики вращательного движения в проекциях на связанные оси

7-12 – кинематические соотношения

7-9 – служат для определения эйлеровых углов

10-12 – служат для определения координат ц.м. () в стартовой с.к.

13-15 – геометрические соотношения, устанавливающие связь между углами, ориентирующие ЛА в различных с.к.

Система I определяет 15 переменных:

 - заданы постоянными

 - определяют продольное движение ЛА

 - определяют боковое движение ЛА

Система I представляет собой сложную систему дифференциальных уравнений, является нелинейной и может быть решена с помощью электронной вычислительной техники. Эта система записана без учёта колебаний жидкого наполнения, влияния упругости корпуса и не учитывает влияние ветра.

Общий вид линейной системы:

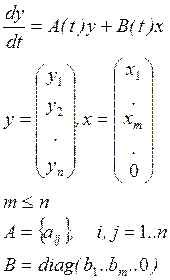
На практике используют упрощённые математические модели, которые, тем не менее, при решении практических задач позволяют получить приемлемые результаты.

Основные методы упрощения

общей пространственной системы.

1. Разделение общего пространственного движения ЛА на движение ц.м. и вращательное движение относительно ц.м.

2. Разделение общего пространственного движения ЛА на продольное и боковое.

3. Линеаризация общей пространственной системы уравнений.

Рассмотрим последовательно эти методы упрощения:

1. Разделение общего пространственного движения ЛА на поступательное движение ц.м. и вращательное движение относительно ц.м.

Между уравнениями, входящими в общую систему I имеются перекрёстные аэродинамические и инерционные связи, а если учитывать уравнение управления, определяющее отклонение углов рулей, то необходимо учитывать перекрёстные связи системы управления по каналам тангажа, рысканья и крена.

В уравнениях динамики перекрёстные инерционные связи проявляются через члены, содержащие или произведения угловых скоростей или центробежные моменты инерции (если они учитываются). Аэродинамические перекрёстные связи проявляются в наличии в уравнениях вращательного движения по крену и рысканью перекрёстных аэродинамических моментов, обусловленных несимметричностью обтекания ЛА в полёте.

Этот метод упрощения производится чаще всего при приближённом решении задачи по определению траектории движения ц.м. ЛА и задач, связанных с устойчивостью движения и с управлением. При расчёте траектории предполагают, что система управления работает идеально, и поэтому можно пренебречь переходными процессами изменения параметров движения ЛА при отклонении органов управления. В идеальной системе управления все элементы, в том числе и сам ЛА (который является звеном контура управления), должны быть безынерционными. В применении к ЛА это означает, что   . Кроме того в выражениях для аэродинамических моментов  можно пренебречь слагаемыми, зависящими от  (демпфирующие моменты),  (моменты от запаздывания скоса потока)

Т.о. вместо 4, 5 и 6 уравнений можно получить балансировочные соотношения:

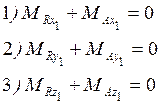
Заменяя моменты тяги  и  эквивалентными  отклонениями рулей можно записать вместо 2 и 3 уравнений следующие балансировочные соотношения: