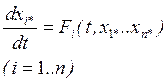
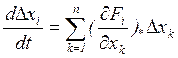 (3)
(3)
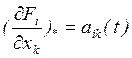
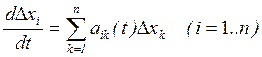
Или в матричной форме:
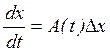 (3')
(3')
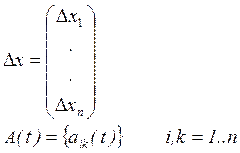
Система (3) (или (3') ) является линейной
системой относительно отклонений ![]() . Она называется
системой уравнений в отклонениях или в вариациях. Коэффициенты этой системы
. Она называется
системой уравнений в отклонениях или в вариациях. Коэффициенты этой системы ![]() , элементы матрицы А, зависят
от параметров невозмущённого движения. Если все параметры невозмущённого
движения являются постоянными (балансировочный режим), то
, элементы матрицы А, зависят
от параметров невозмущённого движения. Если все параметры невозмущённого
движения являются постоянными (балансировочный режим), то ![]() и система (3) будет системой
дифференциальных уравнений с постоянными коэффициентами.
и система (3) будет системой
дифференциальных уравнений с постоянными коэффициентами.
Вывод: т.о. вместо исходной нелинейной системы
(1) относительно фазовых координат ![]() мы получили линейную
систему (3) относительно отклонений (вариаций) этих координат от их значений в
некотором программном невозмущённом движении.
мы получили линейную
систему (3) относительно отклонений (вариаций) этих координат от их значений в
некотором программном невозмущённом движении.
Следует отметить, что метод линеаризации не имеет строгого теоретического обоснования. Его справедливость в каждом конкретном случае должна подтверждаться сравнением решений исходной и линеаризованной системы.
Проведём линеаризацию уравнений пространственного движения I. Пусть невозмущённое движение представляет из себя некоторый заданный полёт в пространстве. Параметры этого движения являются известными функциями времени.
Предположим, что параметры невозмущённого движения в боковом движении
[![]() ] являются малыми величинами.
Т.о. выполняется условие разделения пространственной системы на продольное и
боковое движения. Это предположение принимается для упрощения итоговой системы
в вариациях и не является принципиальным. Будем считать, что
] являются малыми величинами.
Т.о. выполняется условие разделения пространственной системы на продольное и
боковое движения. Это предположение принимается для упрощения итоговой системы
в вариациях и не является принципиальным. Будем считать, что
![]() в возмущённом движении будут
такими же, как в невозмущённом. Кроме того, не будем учитывать влияние высоты
на тягу R и
аэродинамические силы и моменты, т.к. оно не значительно.
в возмущённом движении будут
такими же, как в невозмущённом. Кроме того, не будем учитывать влияние высоты
на тягу R и
аэродинамические силы и моменты, т.к. оно не значительно.
Рассмотрим линеаризацию на примере уравнений продольного движения. Подробно рассмотрим линеаризацию первого уравнения системы (II). Запишем в нормальной форме Коши:
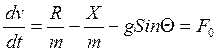
![]() - функция параметров движения ЛА
- функция параметров движения ЛА
![]()
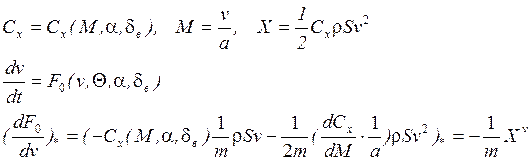
![]() после скобок означает, что все
параметры внутри скобок со
после скобок означает, что все
параметры внутри скобок со ![]()
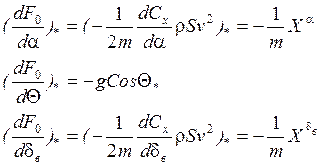
Опуская индекс * и учитывая другие сокращения, понятные из предыдущего изложения, можем записать следующее уравнение в вариациях:
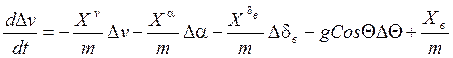
![]() - возмущающая сила, действие
которой не учитывалось в невозмущённом движении.
- возмущающая сила, действие
которой не учитывалось в невозмущённом движении.
Проведём линеаризацию уравнения:
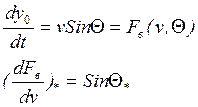
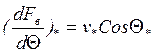
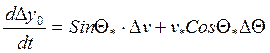
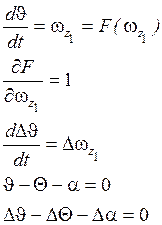
Аналогично производится линеаризация остальных уравнений системы (II).
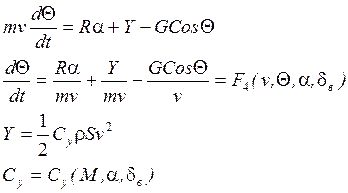
Запишем уравнение продольного движения в вариациях. При этом пронумеруем переменные, входящие в систему (II):
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
Каждому уравнению в вариациях присвоим
соответствующий номер. Например, уравнению, описывающему ![]() , присвоим 0; уравнению, описывающему
, присвоим 0; уравнению, описывающему ![]() - 1 и т. д. Обозначим эти коэффициенты
буквой а.
- 1 и т. д. Обозначим эти коэффициенты
буквой а.
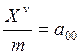 ,
, 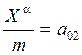 , тогда
система запишется следующим образом:
, тогда
система запишется следующим образом:
Система IV.
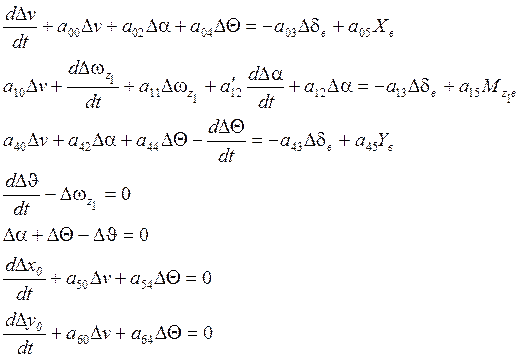
![]() - динамические коэффициенты.
- динамические коэффициенты.
01.04.05
Они выражаются через аэродинамические и инерционные характеристики ЛА следующим образом:
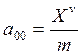 1/c;
1/c; 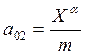 м/
м/![]() ;
; 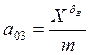 м/
м/![]() ;
;
![]() м/
м/![]() ;
; 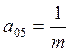 1/кг;
1/кг; 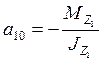 1/м;
1/м;
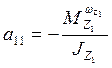 1/с;
1/с; 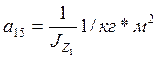 ;
; 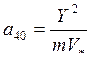 1/м;
1/м;
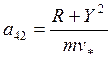 1/с;
1/с; 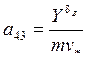 1/с;
1/с; 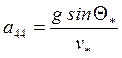 1/с;
1/с;
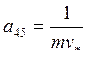 с/кг*м;
с/кг*м; ![]()
![]() м/с;
м/с;
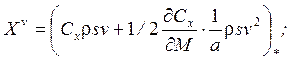
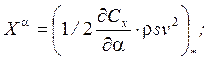
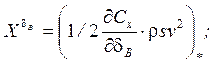
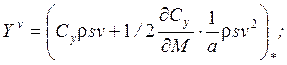
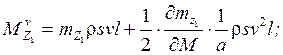
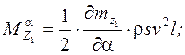
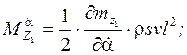
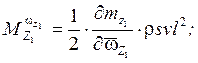
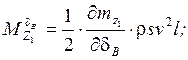
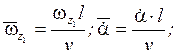
Cx = Cx(M, α, δв);
Cy = Cy(M, α, δв);
![]()
Уравнения бокового движения в вариациях.
В качестве программного (невозмущённого) режима при записи этих уравнений примем так называемый балансировочный режим. Это прямолинейный установившейся полёт на постоянной высоте. Покажем схему полёта в этом режиме:
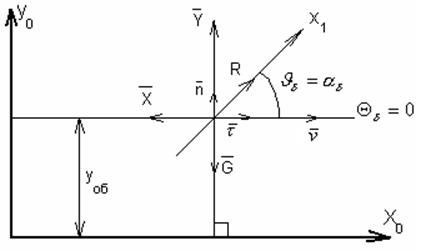
Это установившейся полёт:
(![]() )
)
![]() ;
;
Вводя аналогично предыдущему
динамические коэффициенты ![]() для движения рысканья и
динамические коэффициенты
для движения рысканья и
динамические коэффициенты![]() для движения крена, мы
можем записать уравнения бокового движения в вариациях при этих всех уравнениях.
для движения крена, мы
можем записать уравнения бокового движения в вариациях при этих всех уравнениях.
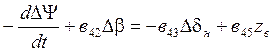 ;
;
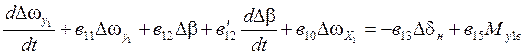 ;
;
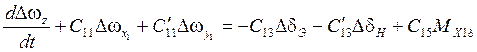 ;
;
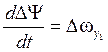 ; (V)
; (V)
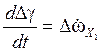 ;
;
![]() ;
;
![]() ;
;
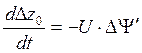 ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.