R=QU+![]()
C подъёмом на высоту ![]() >U
>U
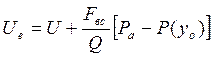
Реактивная сила приложена в центре масс выходного сечения сопла, но не в геометрическом центре.
Вывод уравнения поступательного движения в пространстве.
Для этого используется уравнение Мещерского:
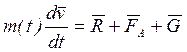 (1)
(1)
![]() - тяга;
- тяга;
![]() -главный вектор аэродинамических
сил;
-главный вектор аэродинамических
сил;
![]() -сила тяжести;
-сила тяжести;
![]() -абсолютное ускорение;
-абсолютное ускорение;
![]() -скорость центра масс
относительно земли (путевая скорость);
-скорость центра масс
относительно земли (путевая скорость);
Уравнение (1) эквивалентно трём уравнениям в проекциях.
Чтобы получить эти уравнения нужно выбрать какую-либо из координатных систем,
рассмотренных нами ![]() выше (были рассмотрены 5
координатных систем: земная, связанная, скоростная, полусвязанная,
полускоростная).
выше (были рассмотрены 5
координатных систем: земная, связанная, скоростная, полусвязанная,
полускоростная).
При выводе уравнений поступательного движения может использоваться любая из пяти рассмотренных систем. Вид уравнений в проекциях будет зависеть от выбора системы координат.
1) ![]() - полускоростная
система координат;
- полускоростная
система координат;
2) ![]() - связанная система
координат;
- связанная система
координат;
Они используются наиболее часто при выводе уравнений поступательного движения.
В уравнении (1) слева стоит полная векторная производная от
вектора ![]() , а справа сумма сил. Если вектор
, а справа сумма сил. Если вектор ![]() записать в проекциях
записать в проекциях ![]() , то полная векторная производная равна
локальной производной
, то полная векторная производная равна
локальной производной 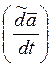 плюс векторное произведение
плюс векторное произведение ![]() , где
, где
![]() - абсолютная угловая скорость
системы координат Oxyz;
- абсолютная угловая скорость
системы координат Oxyz;
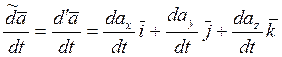 - локальная
производная
- локальная
производная ![]() , если мы орты
, если мы орты ![]() считаем
постоянными, а дифференцируем только проекции;
считаем
постоянными, а дифференцируем только проекции;
первое слагаемое отражает изменение проекции от времени;
второе слагаемое отражает движение системы координат, в которой записывается вектор;
1) Рассмотрим
первый случай: ![]() - совпадает с осью
- совпадает с осью ![]() полускоростной системы координат, т.к.
полускоростной системы координат, т.к. ![]() =х;
=х;
2) Рассмотрим
второй случай: ![]()
Из рис. 3 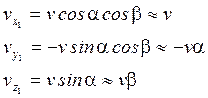
![]() ) Рассмотрим
полускоростную систему координат
) Рассмотрим
полускоростную систему координат ![]() . Полная
производная вектора
. Полная
производная вектора 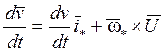 , где
, где ![]() -
абсолютная угловая скорость вращения системы координат
-
абсолютная угловая скорость вращения системы координат ![]() .
.
Абсолютная угловая скорость вращения – это угловая скорость вращения полускоростной системы относительно земной. Земная система координат считается инерциальной, т.е. неподвижной.
![]() - абсолютная угловая
скорость полускоростной системы.
- абсолютная угловая
скорость полускоростной системы.
Запишем векторное произведение в проекциях:
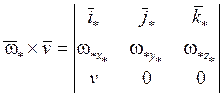 =
=![]()
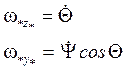
Проекции на ![]()
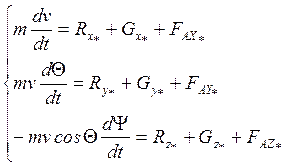
![]() - нормаль,
- нормаль,
![]() - касательная.
- касательная.
22.02.05
![]() ) Рассмотрим связанную
систему координат
) Рассмотрим связанную
систему координат ![]() .
.
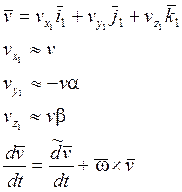
![]()
![]() - абсолютная угловая
скорость системы координат
- абсолютная угловая
скорость системы координат ![]() ;
;
![]()
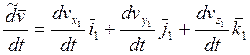 - локальная производная;
- локальная производная;
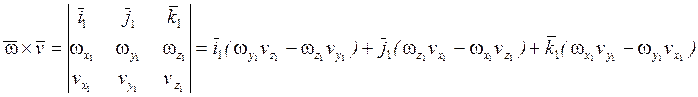
![]()
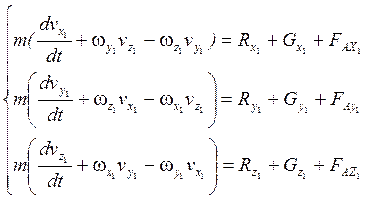
Силы и моменты, действующие на ЛА. Выражение для проекции сил на полускоростные и связанные оси.
Для решения поставленной задачи рассмотрим взаимное расположение связанной, скоростной и полускоростной систем координат.
Рис.3 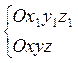
![]()
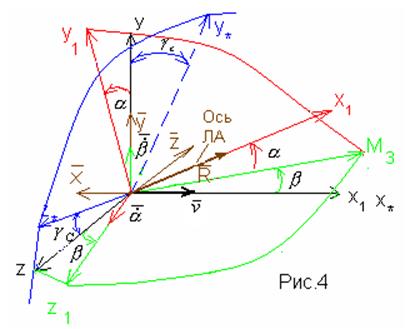
Рассмотрим сначала проекции сил на полускоростные и связанные оси.
![]() - тяга;
- тяга;
Общий метод заключается в следующем:
Сила представляется в проекциях на те координатные оси, в которых она задана.
![]()
Тяга должна сообщать ускорение.
![]() ;
;
![]() - компоненты тяги;
- компоненты тяги;
Они используются для управления вращательным движением ЛА относительно центра масс.
![]()
Будем считать, что ![]() , значит
тяга
, значит
тяга ![]() .
.
Запишем выражение для проекции силы тяги на связанные оси:![]() .
.
Запишем выражение для проекции тяги на полускоростную систему координат. Методика проектирования заключается в следующем.
![]()
Из таблицы 3 ![]()
![]() ;
;
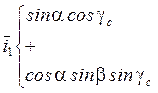
Если ![]() - малы, то
- малы, то ![]()
![]()
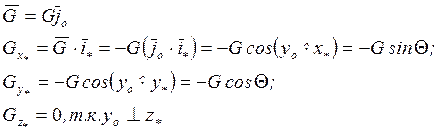
Аэродинамические силы.
Аэродинамические силы являются распределенными.
![]() - суммарная аэродинамическая
сила, являющаяся равнодействующей. Эта равнодействующая приложена в некоторой
точке на оси ЛА, которая является центром давления.
- суммарная аэродинамическая
сила, являющаяся равнодействующей. Эта равнодействующая приложена в некоторой
точке на оси ЛА, которая является центром давления.
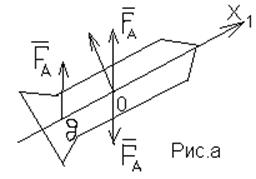
Эту силу, приложенную к центру давления, можно заменить силой, приложенной к центру тяжести и парой. Предыдущая схема эквивалентна следующей схеме:
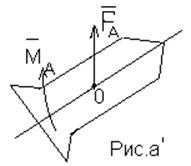
![]() - аэродинамический момент;
- аэродинамический момент;
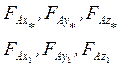
![]()
Oxyz: 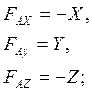
X - сила лобового
сопротивления(против оси ![]() ) ;
) ;
У - подъёмная сила (по оси у);
Z - боковая сила (против оси z);
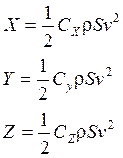
![]() - безразмерные
коэффициенты;
- безразмерные
коэффициенты;
v - скорость центра масс;
![]() - массовая плотность воздуха;
- массовая плотность воздуха;
S - характерная площадь;
![]() > 0; Y
- направлена вверх; Y и Z направлены в ту сторону, чтобы
проекции их на ось
> 0; Y
- направлена вверх; Y и Z направлены в ту сторону, чтобы
проекции их на ось ![]() были положительны.
были положительны.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.