Машиностроение \ Механика полета

Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения, страница 26

Для того, чтобы можно было применить это приём, необходимо, чтобы коэффициенты изменялись медленно. Это означает, что в течении интервала времени, равного времени переходного процесса исследуемой системы, изменение коэффициентов не должно превышать 1520 % от начального значения на указанном интервале.

Справедливость метода «замораживания» коэффициентов должна проверяться каждый раз расчётом некоторых модельных задач для полной нелинейной системы (I) на компьютере.

Теоретический метод этот ничем не обоснован.

03.05.05 *

Продольное возмущённое движение.

Анализ продольного возмущённого движения.

Проведём анализ динамических свойств продольного возмущённого движения ЛА, вызванного внезапным отклонением руля высоты. Будем использовать систему уравнений в вариациях (IV).

Первые 4 уравнения системы можно исследовать независимо от уравнений, описывающих вариации , т.к. эти вариации не входят в указанные 4 уравнения. Кроме того, из этой системы исключим вариацию  с помощью уравнения .

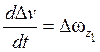Тогда эти уравнения примут следующий вид:

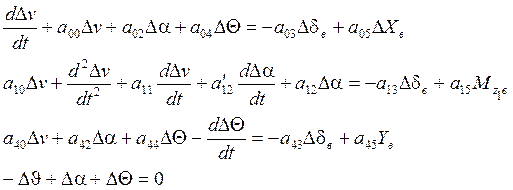                                       (IV’)

Рассмотрим свободное возмущённое движение.

При  получаем однородную систему дифференциальных уравнений.

Если программным движением является балансировочный режим, то .

IV’ – система линейных дифференциальных уравнений с постоянными коэффициентами.

Общее решение этой системы можно записать в следующем виде:

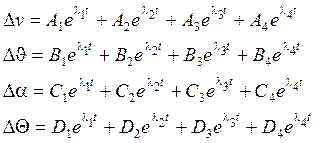
 - корни характеристического уравнения

Характеристическое уравнение:

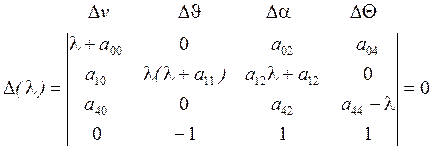
Для устойчивости системы  (необходимое условие устойчивости), они должны быть вещественными; таких корней 4. Все эти корни могут быть:

1) все вещественные, отрицательные;

2) 2 корня вещественные, отрицательные, 2 – комплексные, попарно сопряжённые:

3) все корни комплексные:

В этом случае решение может быть представлено в следующем виде:

                                                                   (*)

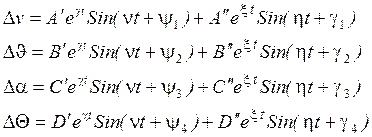Решение представляет собой наложение двух колебательных движений. Вещественная часть характеризует степень затухания свободного возмущённого движения, а коэффициент при мнимой части – его частоту. При этом расчёты показывают, что корни характеристического уравнения по модулю разделяются на 2 больших и 2 малых ( - большие,  - малые,  - большие величины,  - малые). Отсюда следует, что паре больших комплексных корней соответствует быстро затухающее колебательное движение с большой частотой, т.е. с малым периодом 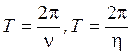. Это движение называется короткопериодическое (быстрое). Паре малых корней соответствует медленно затухающее колебательное движение с малой частотой, т.е. с большим периодом. Такое движение называется длиннопериодическим или фугоидным – медленное движение.

В качестве примера рассмотрим ЛА, летящий на высоте y0=12000 м со скоростью v=800 км/ч. Расчётные значения динамических коэффициентов имеют следующие значения:

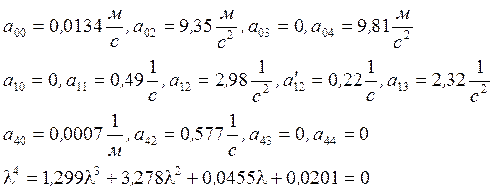
Корни этого уравнения:

Короткопериодическое движение

Длиннопериодическое движение

Корни

Период колебаний Т, с

3,724

80,25

Время уменьшения амплитуды вдвое, с

1,076

123,75

Колебательность К

0,09072

0,638

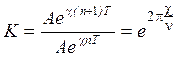
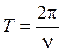
Эти данные взяты из книги Лебедев и Карабанов «Динамика систем управления ЛА».

Анализ решений свободного возмущённого движения для ЛА различных типов и различных случаев невозмущённого полёта показывает, что имеется закономерность не только в величине корней, но и в величине произвольных постоянных интегрирования, которые находятся из начальных условий.

Скачать файл