![]() - ось ЛА;
- ось ЛА;
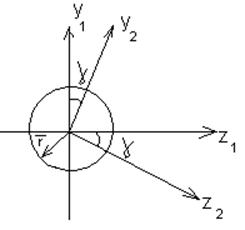
Остальные системы координат из перечисленных выше при записи уравнений вращательного движения не используются. Система связанная неизменно связана с ЛА, т.е. оси связанной системы, при движении ЛА сохраняют относительно него постоянную ориентацию, т.е. связанная система в пространстве вращается с той же угловой скоростью, что и сам ЛА. Таким образом, моменты инерции, которые входят в уравнение вращательного движения, в случае использования связанной системы координат будут зависеть только от изменения массы, и не будут зависеть от вращения ЛА, т.к. оси связанной системы координат сохраняют постоянную ориентацию относительно ЛА.
![]() <
< ![]() (всегда);
(всегда);
![]() ;
;
Если ![]() мало (крен
стабилизирован) - не имеет существенного значения.
мало (крен
стабилизирован) - не имеет существенного значения.
![]() - абсолютная угловая скорость
полусвязанной системы координат;
- абсолютная угловая скорость
полусвязанной системы координат;
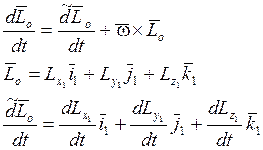
![]() - абсолютная угловая скорость
связанной системы координат (абсолютная угловая скорость ЛА).
- абсолютная угловая скорость
связанной системы координат (абсолютная угловая скорость ЛА).
Примечание: При использовании полусвязанной системы координат
![]()
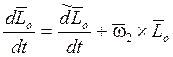
![]() -
момент количества движения ЛА относительно центра масс
-
момент количества движения ЛА относительно центра масс
(кинетический момент);
Эти проекции записываются следующим образом: (для любой конфигурации)
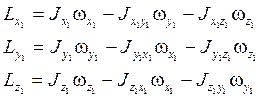
В этих формулах ![]() - абсолютная угловая
скорость ЛА.
- абсолютная угловая
скорость ЛА.
![]() - осевые моменты инерции массы;
- осевые моменты инерции массы;
![]() - центробежные моменты
инерции (произведения инерции);
- центробежные моменты
инерции (произведения инерции);
Осевые моменты инерции определяются следующим образом:
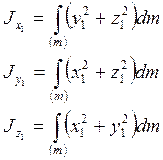
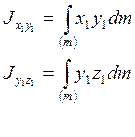 и т.д.
и т.д.
Если ЛА имеет определенную симметрию, то эти формулы упрощаются.
1) ![]() - плоскость симметрии (ЛА
самолётной схемы);
- плоскость симметрии (ЛА
самолётной схемы);
В этом случае все центробежные моменты, содержащие ![]() , обращаются в нуль:
, обращаются в нуль:![]() .
.
Иначе говоря, для самолётной схемы:
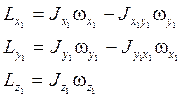
![]() - малые величины
и ими часто пренебрегают.
- малые величины
и ими часто пренебрегают.
2) ![]() - ось симметрии;
- ось симметрии;
В этом случае все центробежные моменты равны нулю.
Если все центробежные моменты инерции относительно осей принятой системы координат равны нулю, то такие оси системы координат называются главными осями инерции.
В этом случае проекции вектора кинетического момента
определяются следующими формулами:![]()
Мы в дальнейшем, при выводе уравнений вращательного движения, будем использовать именно этот случай.
Моменты инерции - есть функции времени ![]() , т.е. являются переменными. Несмотря на
это, при вычислении локальной производной, они выносятся за знак производной.
, т.е. являются переменными. Несмотря на
это, при вычислении локальной производной, они выносятся за знак производной.
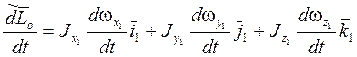 ;
;
Векторное произведение: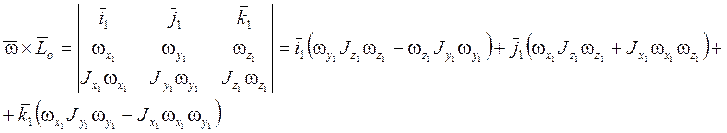
Запишем уравнение вращательного движения в общем виде:
![]()
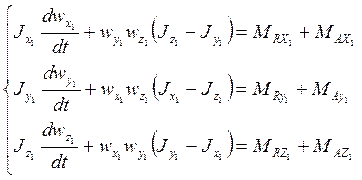 -
уравнения Эйлера;
-
уравнения Эйлера;
![]() - момент тяги;
- момент тяги;
![]() - момент аэродинамических сил;
- момент аэродинамических сил;
Эта система описывает вращательное движение ЛА в пространстве.
![]() ,
,![]() -
управляющие моменты относительно соответствующих осей, которые создаются за
счёт отбора части тяги на управление.
-
управляющие моменты относительно соответствующих осей, которые создаются за
счёт отбора части тяги на управление.
![]() - составляющие аэродинамического
момента, суммарный момент, действующий на ЛА.
- составляющие аэродинамического
момента, суммарный момент, действующий на ЛА.
![]()
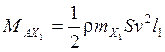 - аэродинамический
момент крена;
- аэродинамический
момент крена;
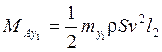 - аэродинамический
момент рысканья;
- аэродинамический
момент рысканья;
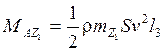 - аэродинамический
момент тангажа (движение тангажа ототносительно
- аэродинамический
момент тангажа (движение тангажа ототносительно ![]() );
);
v - скорость центра масс;
S - характерная площадь;
![]() - массовая плотность
воздуха (среды);
- массовая плотность
воздуха (среды);
![]() - характерная длина;
- характерная длина;
![]() - безразмерные
коэффициенты аэродинамических моментов крена, рысканья и тангажа.
- безразмерные
коэффициенты аэродинамических моментов крена, рысканья и тангажа.
В качестве характерной площади может быть площадь миделя, характерная площадь, диаметральная площадь.
Имеет место следующая преимущественная зависимость этих коэффициентов, которая определяется экспериментально:
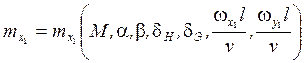 ;
;
![]() -
угол отклонения рулей направления;
-
угол отклонения рулей направления;
![]() - угол отклонения
элеронов;
- угол отклонения
элеронов;
![]() - угол отклонения рулей
высоты;
- угол отклонения рулей
высоты;
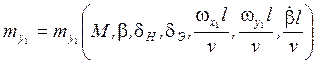 ;
;
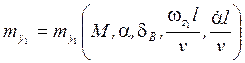 ;
;
Отражает влияние аэродинамических связей, которые являются следствием появления перекрёстных аэродинамических моментов, обусловленных несимметричностью обтекания ЛА в полёте.
4.03.05
На практике, для определения этих коэффициентов, используются линейные аппроксимации:
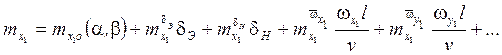
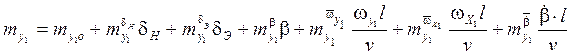
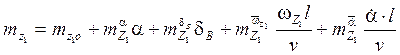
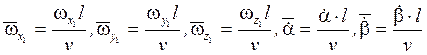
![]() -
угол отклонения рулей направления;
-
угол отклонения рулей направления;
![]() - угол отклонения элеронов;
- угол отклонения элеронов;
![]() - угол отклонения рулей высоты;
- угол отклонения рулей высоты;
![]() - сложная нелинейная
функция, зависящая от
- сложная нелинейная
функция, зависящая от ![]() и
и ![]() . Часто
эту зависимость не учитывают, принимая её постоянной.
. Часто
эту зависимость не учитывают, принимая её постоянной.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.