Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения, страница 19

 - частное решение уравнения (5).

Подставим предполагаемую формулу решения уравнения (6) в уравнение (5), получим:

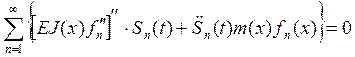                                     (7)

     Из (7) следует, что каждая =0, значит должно выполняться следующее условие:

=0;

Перепишем его следующей пропорцией:

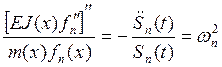;                                                                     (8)

Так как x и t независимые переменные, то отношение функции времени равно отношению функции длины только в том случае, если оба этих отношения постоянны.

Вводя для этой постоянной обозначение   на основании (8), получаем следующие, связанные друг с другом лишь через параметр , обыкновенные дифференциальные уравнения:

                                                                  (9)

                                                                                        (10)

n=1,2...

Принятая форма решения (6) показывает, что уравнение (10) определяет закон колебаний во времени каждой точки другой линии. А уравнение (9) определяет распределение амплитуд колебаний вдоль этой линии.

Решение уравнения (10) - это свободные гармонические колебания.

Сn,  - производные постоянные, находящиеся из следующих начальных условий:

 

Для решения уравнения (9) требуется 4 граничных условия, которые на основании граничных условий (2) и (3) запишутся так:

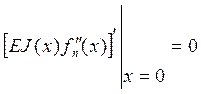                                                (11)

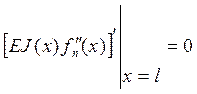                                          (12)

Задача 9+11+12, при любом значении параметра , имеет нулевое решение:

 - это решение называется тривиальным.

Нам нужно отыскать не тривиальное решение. Отыскивание этих решений - есть классическая задача математической физики - задача Штурма-Лиувилля.

Решение этой задачи - функция  - называется собственной функцией, а - собственные значения (это числа, которым соответствуют собственные функции).

В теории колебаний, собственные функции называются ещё формами, собственные значения - частоты свободных колебаний.

Существует бесконечное множество собственных значений  и соответствующих им собственных функций .

Среди множества- есть нулевые. При  =0 уравнение (9) вырождается в уравнение:

                                                    (13)

Непосредственной проверкой можно установить, что линейно независимые функции где

 - координата центра масс балки, удовлетворяющая уравнению (13) и граничным условиям (11) и (12).

В дальнейшем будем считать, что функциям  соответствуют одинаковые перемещения всех точек оси балки, а функции  соответствует перемещение, пропорциональное разности , то есть поворот вокруг центра масс балки как жёсткого тела. Оба этих движения не сопровождаются деформациями корпуса и таким образом собственные значения =0 не определяют изгибных колебаний корпуса.

Собственные значения (n=1,2...), не равные нулю, присущи упругим колебаниям. Все они вещественные и положительные, причём .

Собственные функции , соответствующие различным собственным значениям , ортогональны на отрезке [o,l] c весом m(x).

Условие ортогональности:

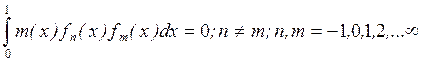                    (14)

Физически условие ортогональности означает, что упругие колебания балки по какому-либо тону, не могут вызвать упругих колебаний других тонов.

12.04.05 *

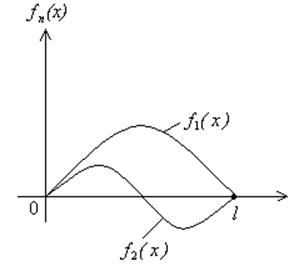
Рассмотрим форму.

Число перемен знака формы n-ого порядка тона равно n-1, иначе говоря узлы n-ой формы делят отрезок [0,l] на n частей.

При нулевых граничных условиях между 2 нулями n-ой формы расположен 1 нуль n+1 формы.

Из уравнения (9) следует, что функция  , где с=const, также удовлетворяет уравнению (9) и граничным условиям (11) и (12). Т.о. задача 9+11+12 определяет форму  с точностью до постоянного множителя с. Чтобы устранить эту неопределённость, производят их нормирование. Вводят понятие нормированной формы:

       

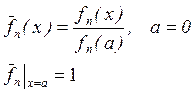
В дальнейшем не будем делать различия между  и .

Задача 9+11+12 имеет точное аналитическое решение для однородной балки, у которой  и  ( - изгибная жёсткость).

Если балка неоднородная, то точного аналитического решения не существует.