Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения, страница 17

Эти динамические коэффициенты , , которые определяются в этих уравнениях следующим образом:

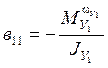  1/с;     ;       1/;

   1/;        1/с;         1/;

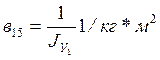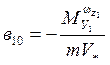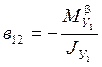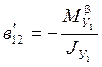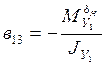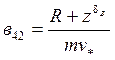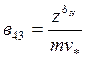  1/с;        1/с; 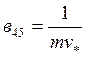            с/кг*м;             

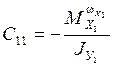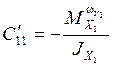   1/с;      1/с;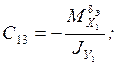        

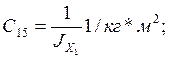
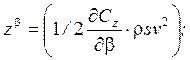
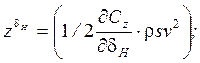
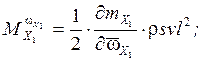
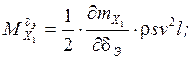
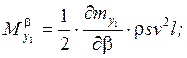
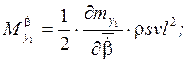
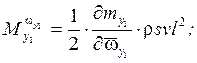
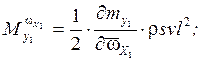
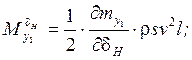
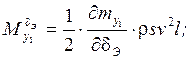
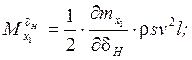
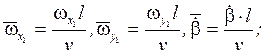
Учёт влияния вращающихся масс в уравнениях вращательного движения ЛА.

Пусть имеется в ЛА система из трёх маховиков, которые ориентированы симметрично по осям так, что система координат по OXYZ остаётся главной осью инерции, центробежные моменты отсутствуют.

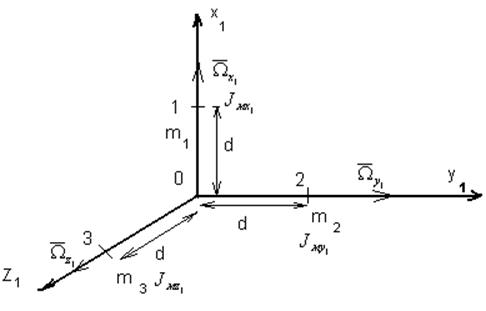
Масса маховиков мала . Маховики вращаются относительно соответствующих осей.

- угловые скорости вращения маховиков относительно ЛА.

Сам ЛА вращается с угловой скоростью  вместе с маховиками.

Нужно составить уравнение вращательного движения вместе с маховиками. Они используются для управления в космосе.

Будем считать, что на ЛА действует система внешних сил.

 - аэродинамический момент;

 - момент тяги;

Уравнение вращательного движения: 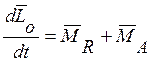                         (1)

-  момент количества движения ЛА вместе с маховиками (кинетический момент);

Полная векторная производная:

;               - ?

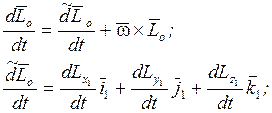
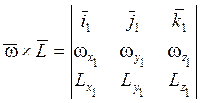Запишем уравнение вращения для проекций с маховиками.

Обозначим:

 - моменты инерции относительно  соответственно без маховиков.

- момент инерции всех маховиков относительно .

;

Тогда с учётом этих обозначений запишем момент инерции ЛА вместе с маховиками:

;

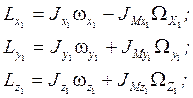
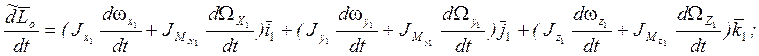
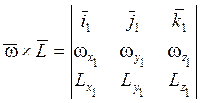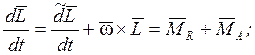
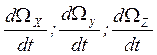
Кроме того, в уравнение будут входить гироскопические моменты, содержащие произведения угловых скоростей.

05.04.05 *

Учёт влияния ветра в задачах динамики полёта.

Введём следующие понятия:

 - скорость ц.м. относительно Земли (путевая скорость)

 - скорость ц.м. ЛА относительно ветра (воздуха) – воздушная скорость

 - скорость ветра относительно Земли

                                                                                                                           (1)

Учёт влияния ветра будем рассматривать на примере уравнений продольного движения.

Существует 2 способа описания движения ЛА при наличии ветра.

Первый способ основан на рассмотрении относительного движения ЛА по отношению к ветру (метод Дидиона).

Второй способ основан на рассмотрении абсолютного движения ЛА по отношению к Земле, которая считается неподвижной.

Основная идея учёта влияния ветра состоит в том, что аэродинамические силы и моменты, действующие на ЛА определяются величиной и ориентацией вектора воздушной скорости.

Рассматривается плоское движение; будем считать, что в стартовой с.к. скорость ветра задана 2 компонентами:

Рассмотрим следующую схему:

 - плоскость симметрии ЛА

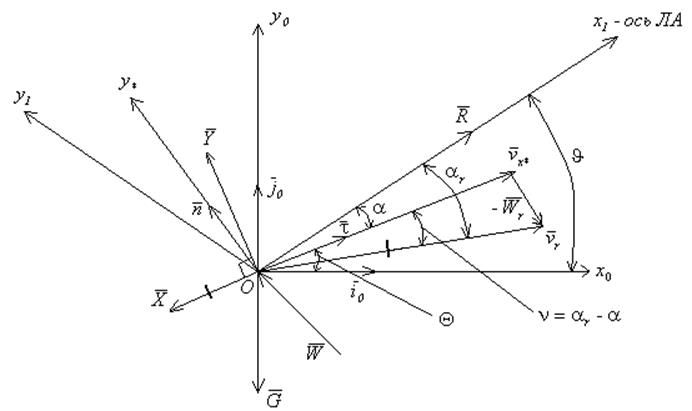
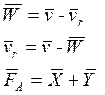
 направлен против

 - угол атаки для воздушной скорости

             

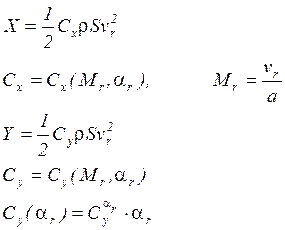
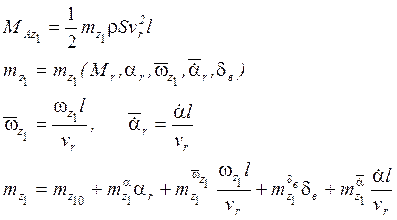
Установим связь между  и ,   и . Для решения этой задачи воспользуемся уравнением (1), которое перепишем:

                                                                                                     (2)

Для решения поставленной задачи спроектируем векторное уравнение (2) на оси связанной с.к. (на x₁ и y₁):

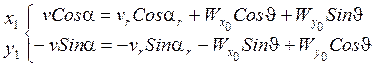
,  - неизвестные

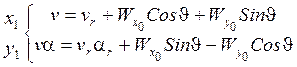
Т.к. по модулю , то можно считать, что

Отсюда:

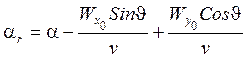
Обозначим разность углов

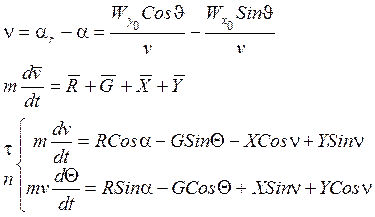
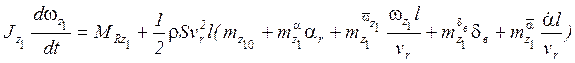
Остальные уравнения остаются без изменения:

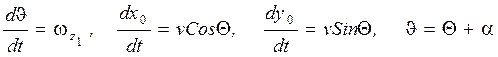
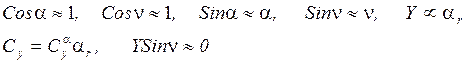
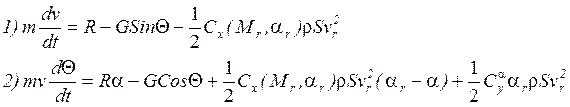
08.04.05

Учёт влияния упругости корпуса в уравнениях динамики.

Тенденция к повышению лётных качеств ЛА за счёт уменьшения отношения веса топлива к весу конструкции, при заданной полезной нагрузке и дальности полёта приводит к уменьшению жёсткости конструкции ЛА. ЛА в полёте подвергается упругим деформациям, имеют место поперечные, продольные и крутильные колебания конструкции. Особенно это относится к ЛА большой длины.

Баллистические ракеты и ракетоносители на некоторых участках полёта проектируются как статически неустойчивые. Для их стабилизации, система угловой стабилизации должна обладать большим коэффициентом усиления и следовательно широкой полосой пропускания частот.