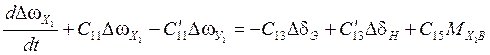 (4)
(4)
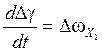
![]() , при этом
, при этом 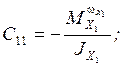
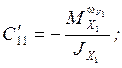
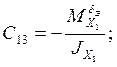
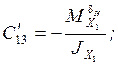
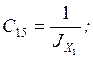
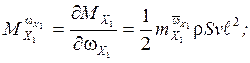
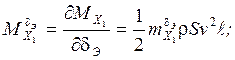
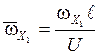 ;
;
Систему (4) можно представить в следующем виде:
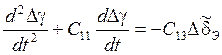 (5),
где
(5),
где
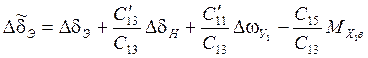 - эквивалентное
отклонение элеронов, учитывающее влияние движения рысканья, а также возмущающий
момент
- эквивалентное
отклонение элеронов, учитывающее влияние движения рысканья, а также возмущающий
момент ![]() .
.
Передаточные функции, соответствующие уравнению (5), найдём, преобразовав это уравнение по Лапласу при нулевых начальных условиях, получаем:
![]() (6)
(6)
Отсюда находим ПФ 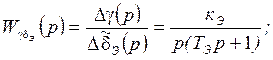 (7),
где
(7),
где
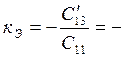
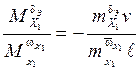 - коэффициент усиления ЛА по движению
крена;
- коэффициент усиления ЛА по движению
крена;
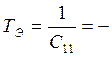
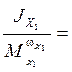 - постоянная времени, характеризующая
протекание переходного процесса по движению крена;
- постоянная времени, характеризующая
протекание переходного процесса по движению крена;
=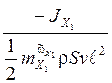 ;
;
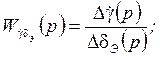
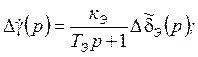
![]() =
= ![]()
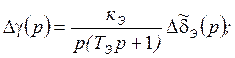
![]()
![]() =
const;
=
const; 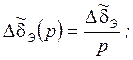
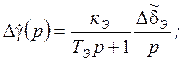
По предельной теореме найдём
установившееся ![]() =
=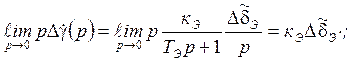
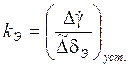 ;
;
Передаточная функция ЛА с учётом упругих поперечных колебаний корпуса.
ПФ ЛА как звена контура управления, необходимо знать для нахождения частотных характеристик системы угловой стабилизации.
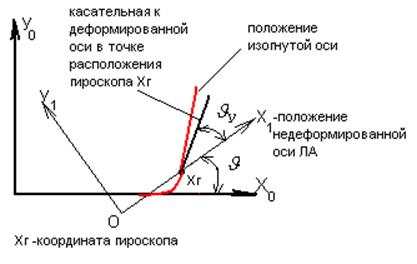
Рассмотрим особенности входного сигнала автомата угловой стабилизации, возникающие в результате влияния на него упругих поперечных колебаний корпуса. Измеритель угла тангажа установлен в некотором произвольном сечении корпуса ЛА, регистрирует две составляющие угла поворота этого сечения относительно инерциальной системы координат.
Первая составляющая соответствует углу поворота недеформируемого корпуса ЛА.
Вторая составляющая - дополнительному повороту данного сечения в результате изгиба корпуса.
Таким образом, обозначить суммарный угол,
регистрируемый датчиком гироскопа через ![]() ,
выражение для этого угла можно записать в виде
,
выражение для этого угла можно записать в виде 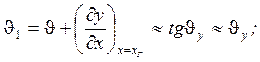
У2 - обусловлено вынужденным колебанием;
у=у1+у2;
Угол между касательной к изогнутой оси корпуса в месте установленного гироскопа и осью недеформируемого корпуса.
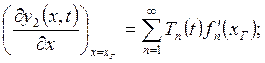
fn(x) - форма свободных колебаний;
Значит ![]()
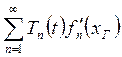 ;
(8)
;
(8)
Преобразуем это уравнение по Лапласу, получаем:
![]()
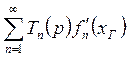 ;
(9)
;
(9)
На основании формулы (9), запишем выражение для ПФ ЛА от
входа ![]() к выходу
к выходу ![]() . Это
будет вот такая ПФ:
. Это
будет вот такая ПФ:
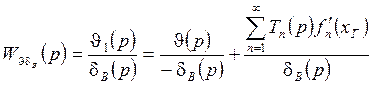 , где
, где
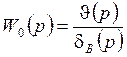 - ПФ жёсткого ЛА.
- ПФ жёсткого ЛА.
Если обозначить 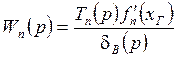 , то
, то
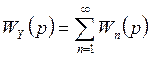 - дополнительная ПФ, вызванная
упругими поперечными колебаниями корпуса.
- дополнительная ПФ, вызванная
упругими поперечными колебаниями корпуса.
![]() =
= ![]() +
+![]() (10)
(10)
Структура, определяемая формулой (10), показывает,
что при учёте упругости корпуса, к звену ![]() ,
представляющему на структурной схеме жёсткий ЛА, параллельно подсоединяется
столько звеньев с ПФ
,
представляющему на структурной схеме жёсткий ЛА, параллельно подсоединяется
столько звеньев с ПФ ![]() , сколько тонов упругих
колебаний учитывается в расчёте. Таким образом
, сколько тонов упругих
колебаний учитывается в расчёте. Таким образом
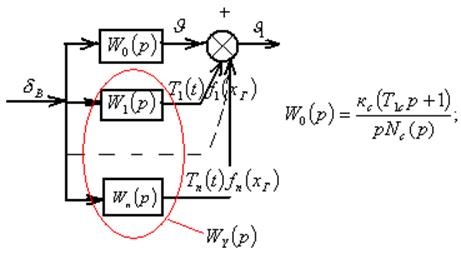
На практике учитывается, как правило, не более двух тонов.
Вид ПФ n - го тона ![]() упругих колебаний зависит от принятой
модели колебаний. Для определения
упругих колебаний зависит от принятой
модели колебаний. Для определения ![]() обратимся к ранее
полученным соотношениям.
обратимся к ранее
полученным соотношениям.
24.05.05 *
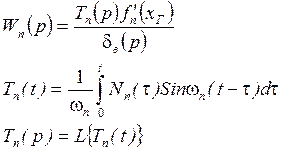
Свёртка 2 функций:
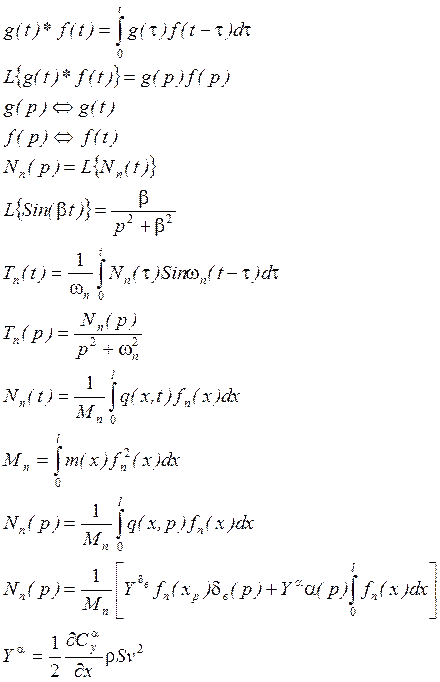
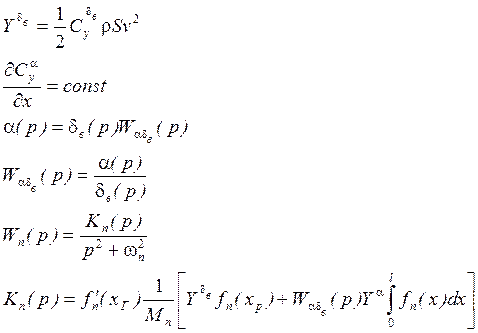
![]() - форма свободных колебаний n-ого тона.
- форма свободных колебаний n-ого тона.
При учёте внутреннего конструкционного демпфирования материала конструкции:
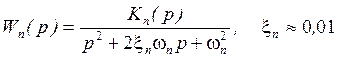
Передаточные функции жёсткого ЛА с учётом колебаний жидкости в баках.
Была рассмотрена маятниковая модель, учитывалось колебание жидкости в одном баке, учитывался первый тон колебаний.
Рассмотрим, как изменится ПФ жёсткого ЛА, если учитывать колебания жидкости.
Система уравнений в вариациях, соответствующая короткопериодическому движению, при учёте колебаний жидкости в 1 баке запишется в следующем виде:
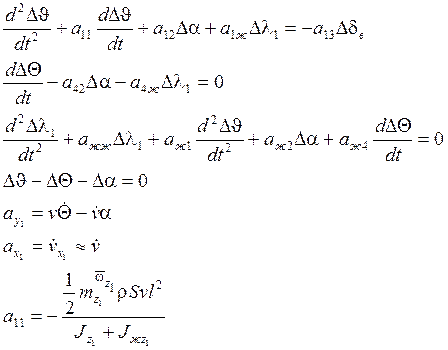
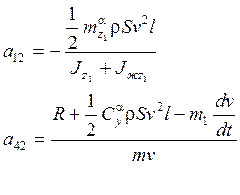
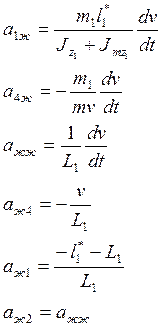
Далее с этой системой поступаем также, как и при выводе ПФ жёсткого ЛА без учёта колебаний жидкости, т.е. преобразуем её по Лапласу при нулевых начальных условиях. При этом вместо системы дифференциальных уравнений получаем систему алгебраических уравнений относительно изображений по Лапласу. Решаем систему по правилу Крамера и находим изображения по Лапласу всех переменных.
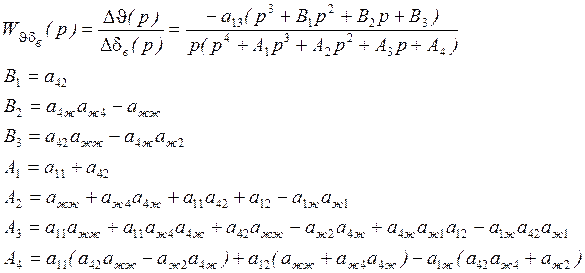
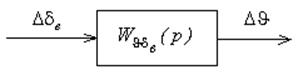
Если положить в последних формулах для ![]() все динамические коэффициенты с индексом
«ж» равными нулю, то:
все динамические коэффициенты с индексом
«ж» равными нулю, то:
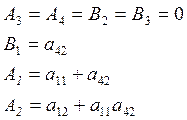
Тогда получим:
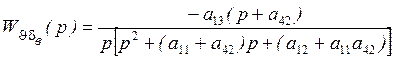 - формула для ПФ жёсткого ЛА
- формула для ПФ жёсткого ЛА
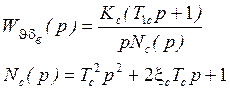
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.