Математическая модель пространственного движения жёсткого ЛА с переменной массой без учёта колебаний жидкого наполнения, страница 28

Для упрощения анализа процессов стабилизации углового положения, часто схематизируют продольное возмущённое движение ЛА, рассматривая только первый этап этого движения, на котором можно пренебречь вариацией скорости, т.е. считать , кроме того, можно не учитывать влияния силы тяжести и аэродинамического момента от запаздывания скоса потока. В уравнениях (IV’) это соответствует тому, что  и . Кроме того, будем считать, что подъёмная сила в основном определяется углом атаки  и слабо зависит от угла поворота руля высоты, то есть будем принимать, что  (случай ЛА типа «поворотное крыло» не рассматривается). Таким образом, при анализе процессов стабилизации будем использовать «усечённую» систему уравнений следующего вида:

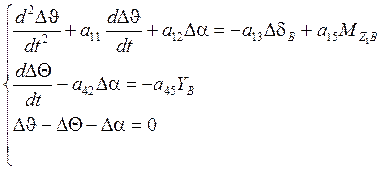                                          (1)

Динамические коэффициенты, входящие в эту систему , принимаем постоянными, считая, что невозмущённое движение представляет из себя балансировочный режим. Найдём, используя систему (1), передаточные функции ЛА для параметров  по отношению к .

Передаточные функции ЛА для продольного возмущённого движения.

Будем использовать систему (1) предыдущего параграфа. Предварительно примем, что . Запишем эту систему в преобразованном по Лапласу виде при нулевых начальных условиях.

Р - аргумент преобразования Лапласа.

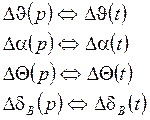
и так далее.

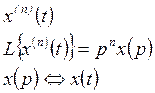
Изображение Лапласа n - ой производной при нулевых начальных условиях:

.

Запишем, используя это,  систему (1) в преобразованном по Лапласу виде. Применим, оператор Лапласа к левой и правой части. Используется теорема линейности:

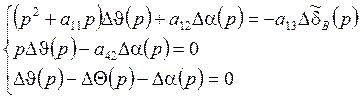                                           (2)

Система уравнений, где  - эквивалентное вариации угла отклонения руля, учитывающее действующий возмущающий момент .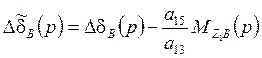

Система (2) является линейной алгебраической системой относительно изображений по Лапласу. Таким образом, применив преобразование Лапласа к системе (1), мы вместо линейной системы дифференциальных уравнений получили линейную алгебраическую систему относительно изображений по Лапласу исходных переменных.

Решим эту систему и найдём искомые переменные в зависимости от  и определим соответствующие передаточные функции. По определению передаточных функций, как известно, передаточная функция от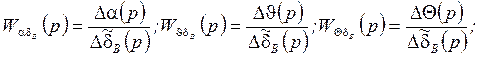  

В дальнейшем изложении упустим для сокращения записи индекс «» и не будем делать различий между  и . Систему (2) будем решать по правилу Крамера. Используя правило Крамера:

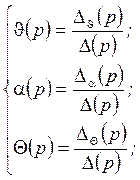, где (р) - главный определитель системы из коэффициентов при переменных, стоящих в левой части.

                 

(р)=;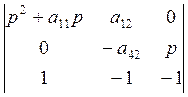

Раскрывая этот определитель, получаем:

, где .

Остальные определители получаются следующим образом:

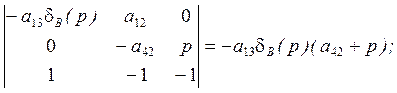
(р)=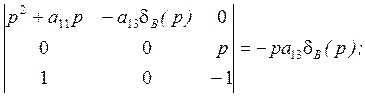 

(р)=

(р)=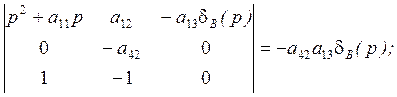 

Теперь можем найти искомые передаточные функции, они запишутся следующим образом:

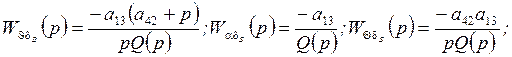
Перепишем полученное выражение, вводя передаточные функции типовых звеньев. Введём обозначения:

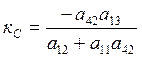 - коэффициент усиления ЛА (снаряда);

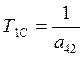  - скоростная постоянная времени;

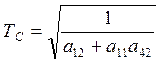 - постоянная времени ЛА;

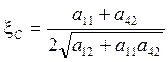 - коэффициент демпфирования;

Тогда, после несложных преобразований, получим следующие выражения для ПФ:

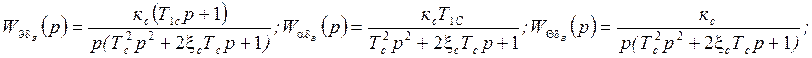
Например, рассмотрим, как выводится одна из найденных передаточных функций:

    

 

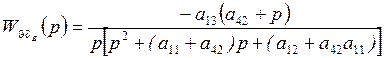
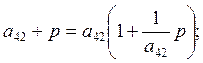
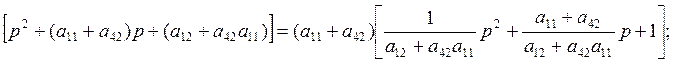
Таким образом, мы можем записать:

 

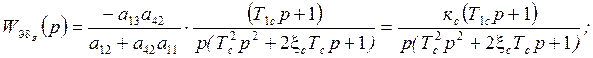
На основании полученных передаточных функций, можно получить и другие передаточные функции, например:

           

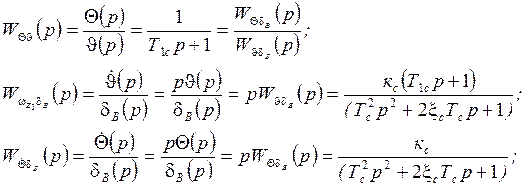
Динамику ЛА можно заменить при воздействии  и входа, вот таким звеном:

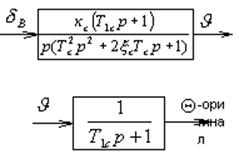
ПФ - это оператор.

Зная передаточную функцию, можно восстановить дифференциальное уравнение, связывающее переменные: вход и выход звена.

()=

 

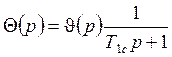
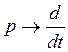
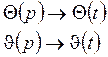
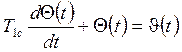
Таким образом, на основании передаточных функций, можно восстановить дифференциальные уравнения, связывающие вход и выход. Аналогично и для других передаточных функций.

17.05.05 *

Физический смысл коэффициентов, входящих в состав передаточной функции.

Пусть .

Преобразование Лапласа:

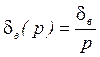
Установим физический смысл . Для этого воспользуемся передаточной функцией:

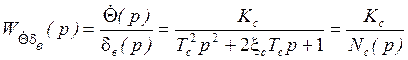
Для сокращения записи обозначим: