при К=3.
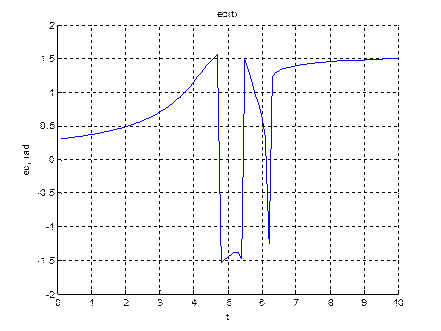
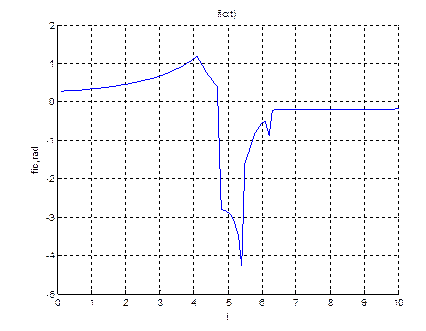
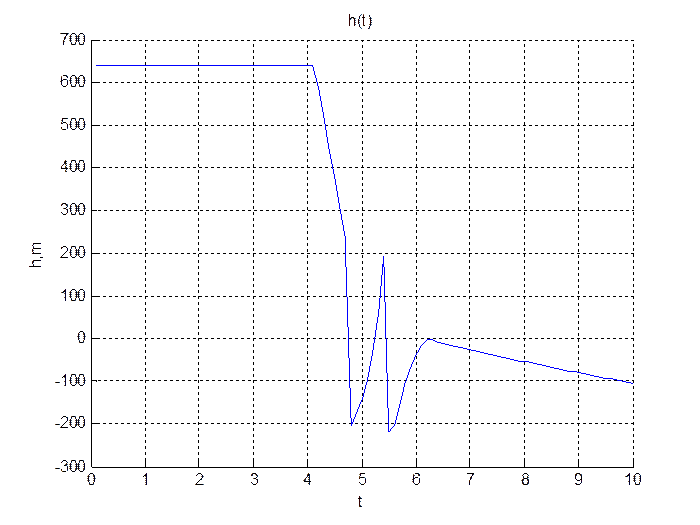
Для К=3.
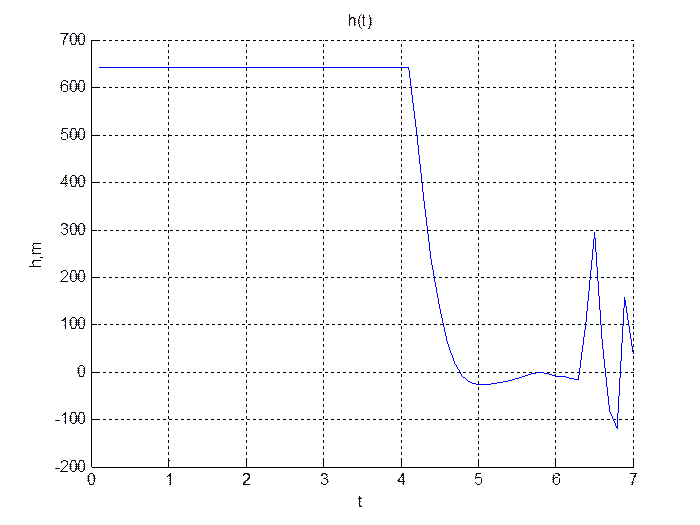
Для К=6.
При К=6.
clear all
clc
%метод пропорционального наведения переходит в метод погони
teta0=0.03 % начальный угол между 0 и вектором скорости рад.
V=436 % начальная скорось в м\с.
x10=0 % координата ЛА, м.
y0=100 % начальная координата ЛА, м.
t1=4 %время, через которое начинается самонаведение, сек.
xc0=2200 % начальные координаты цели в метрах.
yc0=800 %
tetac0=3.1416; % начальный угол движения цели в рад.
Vc=55 % начальная скорось движения цели м\сек
g=9.81
n=0;
m=7; %время для построения графиков в секундах
global teta0 x0 y0 xc0 yc0 V t1 tetac0 Vc g n
figure
x0=[teta0 x10 y0 xc0 yc0 ]% нач знач.
[t,x]=ode23('sistema',[0:0.1:m], [x0]);
plot(t,x(:,1)) %график скорости от времени
grid on;
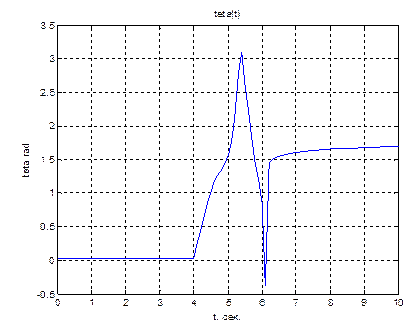
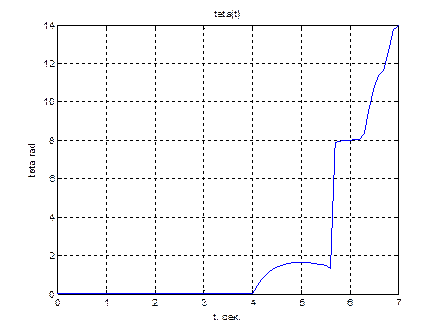
title('teta(t)');
xlabel('t, сек.');
ylabel('teta rad');
hold on
for i=1:1:m*10;
r(i)=sqrt((x(i,2)-x(i,4))^2+(x(i,3)-x(i,5))^2);
ec(i)=atan((x(i,5)-x(i,3))/(x(i,4)-x(i,2)));
fic(i)=ec(i)-x(i,1);
razn(i)=ec(i)-fic(i);
pr(i)=V*sin(ec(i)-x(i,1))-Vc*sin(ec(i)-tetac0); % Vot*sin(mu)=r*ec'
Vot(i)=sqrt(V^2+Vc^2-2*V*Vc*cos(x(i,1)-tetac0));
h(i)=r(i)*pr(i)/Vot(i);
end
i=1:1:m*10;
tt=i/10;
figure
grid on;
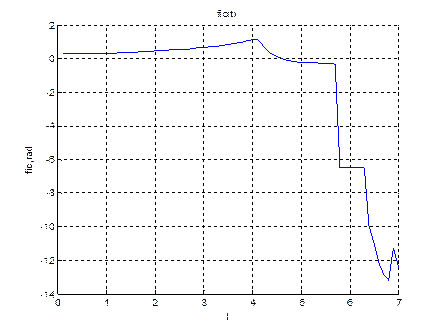
title('fic(t)');
xlabel('t');
ylabel('fic,rad');
hold on
plot(tt,fic(i))
figure
grid on;
title('h(t)');
xlabel('t');
ylabel('h,m');
hold on
plot(tt,h(i))
figure
grid on;
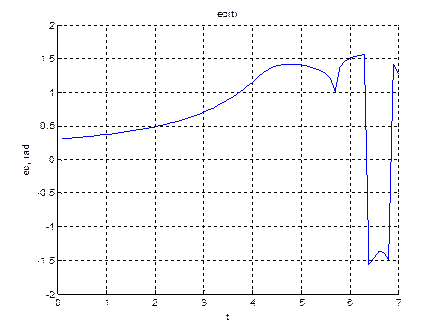
title('ec(t)');
xlabel('t');
ylabel('ec, rad');
hold on
plot(tt,ec(i))
figure
grid on;
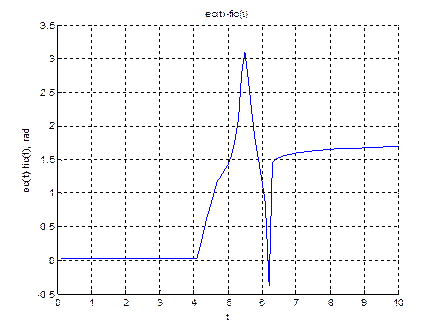
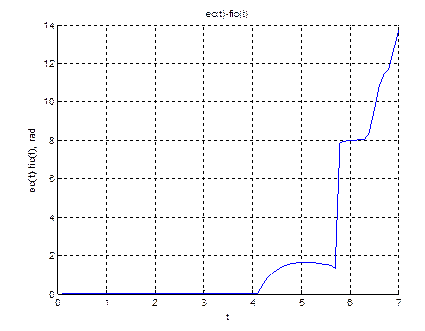
title('ec(t)-fic(t)');
xlabel('t');
ylabel('ec(t)-fic(t), rad');
hold on
plot(tt,razn(i)) %
figure
grid on;
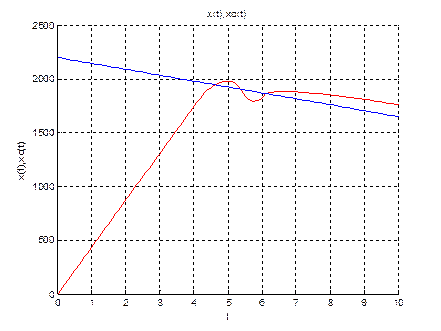
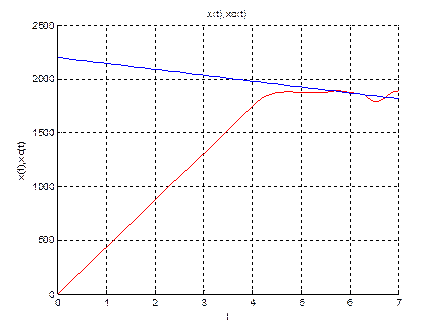
title('x(t),xc(t)');
xlabel('t');
ylabel('x(t),xc(t)');
hold on
plot(t,x(:,2),'red') %график
plot(t,x(:,4))
figure
grid on;
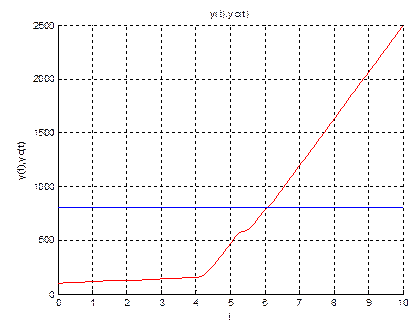
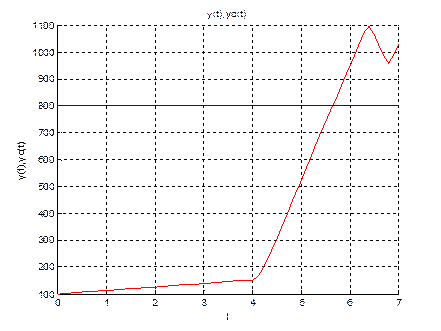
title('y(t),yc(t)');
xlabel('t');
ylabel('y(t),yc(t)');
hold on
plot(t,x(:,3),'red') %графиk
plot(t,x(:,5))
function sistema=pol(t,x);
global teta0 x0 y0 xc0 yc0 V t1 tetac0 Vc g n
k=6;
if t>0
n=n+1;
r(n)=sqrt((x(2)-x(4))^2+(x(3)-x(5))^2);
ec(n)=atan((x(5)-x(3))/((x(4)-x(2))));
fic(n)=ec(n)-x(1);
end
if t<=t1
sistema=[0; V*cos(x(1)); V*sin(x(1)); Vc*cos(tetac0); Vc*sin(tetac0)];
else % метод пропорционального сближения переходящий в метод погони
sistema=[k*(V*sin(fic(n))-Vc*(ec(n)-tetac0))/r(n); V*cos(x(1)); V*sin(x(1)); Vc*cos(tetac0); Vc*sin(tetac0)];
end
end
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.