Теоретическое определение параметров процесса резания ширина и толщина среза при несвободном резании. Теоретический метод определения обрабатываемости материалов резанием, страница 7

Очень часто имеет место хорошая соизмеримость при резании коэффициентов трения  и  на задней и передней поверхностях инструмента. Поэтому при приближенных расчетах, в формулу (51) можно подставлять значения  = , определяемые по формуле (26). Средние контактные напряжения на задней поверхности определяются выражениями

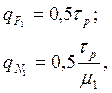                                          (52) , (53)    где и — соответственно среднее тангенциальное и нормальное напряжения.

ТЕМПЕРАТУРА В УСЛОВНОЙ ПЛОСКОСТИ СДВИГА

Количество тепла, выделяющееся в условной плоскости сдвига при резании, равно [40]

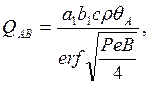                                                       (54)

где — максимальная температура первичных пластических деформаций в условной плоскости сдвига (в точке А, т. е. на режущей кромке), °С.

Механическая энергия пластического деформирования материала в условной плоскости сдвига л вблизи нее равна

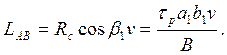                                      (55)

Из равенства механической и тепловой энергий L_AB = Q_AB получаем

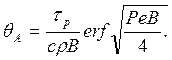                                                    (56)

Формула (56) показывает, что максимальная температура в условной плоскости сдвига определяется механическими  и термическими свойствами  обрабатываемого материала, режимами резания и степенью пластического деформирования материала. Заметим, что при увеличении режимов резания  произведение Ре В быстро увеличивается, при этом возрастает и значение функции erf x. При  функция 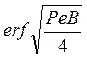становится равной 1, значение максимальной температуры пластических деформаций стабилизируется и определяется более простым выражением для этого предельного состояния

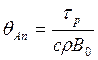                                                       (57)

где B₀ —тангенс угла наклона плоскости сдвига, соответствующего моменту стабилизации температуры

Проведенные по уравнению (56) расчеты температуры  с использованием опытных значений В для различных сталей к сплавов при широком диапазоне изменения Ре показали, что при Ре В 20 величина ее практически не зависит от параметров резания и приближенно может считаться своего рода постоянной характеристикой обрабатываемого материала. Для стабилизированного (предельного) значения   можно написать выражение

                                                                                          (58)

где k —коэффициент, имеющий постоянное значение для данного материала; —температура плавления обрабатываемого материала, °С.

Коэффициент k имеет для всех обрабатываемых материалов одно и то же постоянное значение, равное  k=0,215 [5]. В этом случае предельное значение тангенса  угла наклона условной плоскости сдвига может быть определено    по известным до опыта величинам    из простой формулы

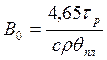                                 (59)

Выражение для текущей температуры, развивающейся на условной плоскости сдвига АВ, получено в виде

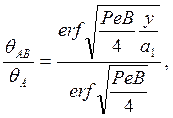                                     (60)

где y — переменная вертикальная координата (рис. 11).

 

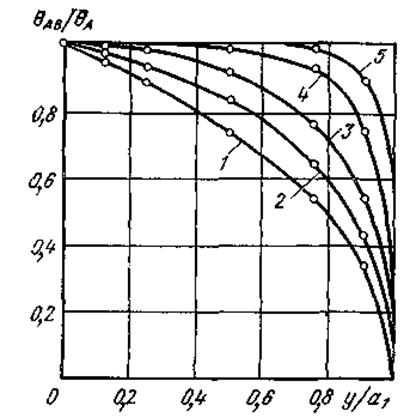Рис. 11.   Изменение относительной температуры  в плоскости сдвига:

1- PeB=1; 2- PeB=5; 3- PeB=10; 4- PeB=25; 5- PeB=50

Формула (60) и рис. 11 показывают, что температура условной плоскости сдвига АВ является переменной и изменяется от 0 в точке В (у=а₁) до максимального значения   в точке А (y = 0).

В условной плоскости сдвига АВ для средней температуры первичной деформации получено выражение [40]

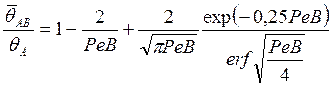                      (61)

Анализ формулы (61) показывает, что влияние третьего слагаемого при РеВ20 является незначительным, поэтому при; приближенных расчетах в области рациональных режимов резания можно пользоваться более простым выражением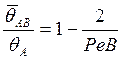                                   

Получены также из выражения (61) следующие степенные формулы:

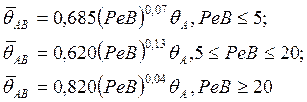                                        (62)

Из формул (62) следует, что при увеличении режимов резания a₁ увеличивается значение комплекса 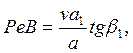и средняя температура в условной плоскости сдвига  постепенно приближается по своему значению к максимальной температуре первичных пластических деформаций