Надежность и долговечность деталей машин в значительной степени определяются качеством поверхностного слоя и, в частности, уровнем и законом остаточных напряжений. Поэтому исключительно важное значение приобретает проблема управления технологическими процессами обработки деталей с получением заданного но условиям долговечности качества поверхностного слоя. Чтобы разработать надежные и эффективные принципы управления качеством поверхностного слоя при механической обработке, необходимо знать общие закономерности протекания изучаемых процессов, располагать широкими научными взаимосвязями между всеми основными технологическими параметрами, устанавливаемыми на основе результатов новейших исследований физической сущности процессов резания и достаточно точного их математического описания.
К настоящему времени выполнено большое количество экспериментальных исследований по определению остаточных напряжений, глубины и степени наклепа, шероховатости поверхности и других параметров поверхностного слоя [13, 18, 25, 29, 55].
Совершенно недостаточно выполнено научных работ по установлению обобщенных аналитических зависимостей параметров поверхностного слоя от технологических условий, что затрудняет решение задачи по назначению режимов резания, обеспечивающих требуемые из соображений долговечности и надежности свойства металла поверхностного слоя.
Ниже рассматривается теоретический метод определения остаточных напряжений при точении сталей и сплавов с учетом температурного и силового факторов [43, 44], а также напряжений от фазовых и Микроструктурных превращений.
|
![]() (234)
(234)
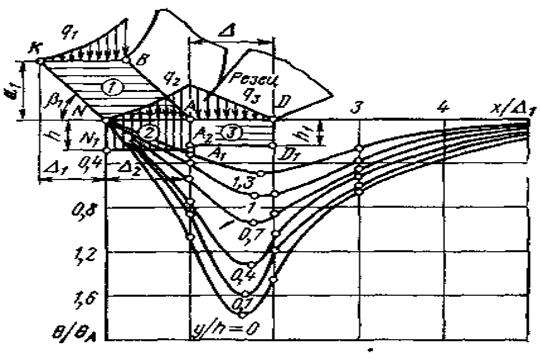
где θ1 – температура от источника ABKNA, возникающего в-)не основных пластических деформаций снимаемого припуска являющегося следствием процессов пластических сдвигов при образовании элементов стружки;
θ2 – температура от источника ANN1A1A, возникающего в зоне поверхностного слоя с опережающими пластическими деформациями;
θ3 – температура источника ADD1A2A возникающего в зоне контакта задней поверхности инструмента с обрабатываемой поверхностью и являющегося следствием процессов трения и пластических деформаций контактирующих поверхностей.
Интенсивности тепловыделения источников 1, 2 и 3 вдоль их соответственно определяются выражениями
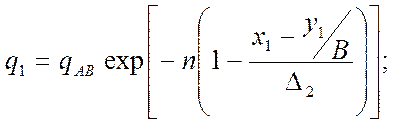 (235)
(235)
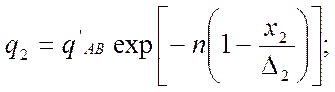 (236)
(236)
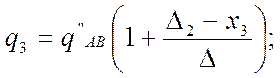 (237)
(237)
где 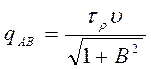 –
интенсивность тепловыделения в плоскости сдвига АВ, Дж/(м2•с);
–
интенсивность тепловыделения в плоскости сдвига АВ, Дж/(м2•с);
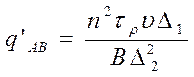 –
интенсивность второго объемного источника тепла, Дж/(м3-с);
–
интенсивность второго объемного источника тепла, Дж/(м3-с);
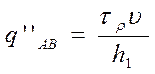 –
максимальная интенсивность третьего объемного источника тепла, Дж/(м3-с);
–
максимальная интенсивность третьего объемного источника тепла, Дж/(м3-с);
![]() e – протяженность наклонного источника вдоль оси x; Δ1 – проекция плоскости сдвига на ось x;
e – протяженность наклонного источника вдоль оси x; Δ1 – проекция плоскости сдвига на ось x;
h – глубина источника NN1A1AN;
h1 – глубина источникаAA2D1DA;
x, x1, x2 и x3 – переменные координаты, отсчитываемые соответственно от точек К и N.
Было осуществлено двойное интегрирование по координатам x0 и y0 исходного уравнения (238), описывающего температурное поле вокруг быстродвижущегося в бесконечном теле линейного источника тепла:
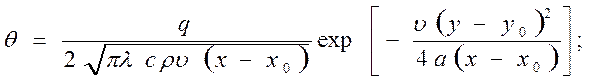 (238)
(238)
где q – интенсивность линейного источника, Дж/мс.
При интегрировании вместо q подставлялись выражения (235), (236) и (237) при x0=x1, x2, x3 и y0=y1 (например, q=q1x0dy0 и т. д.). В результате интегрирования было получено сложное уравнение в конечной форме для суммарной температуры, которое в общем виде представляет собой функцию от «большого количества безразмерных комплексов
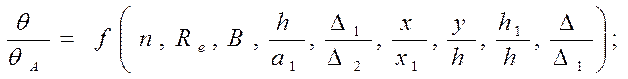 (239)
(239)
где θA – максимальная температура объемных пластических .деформаций зоны металла, расположенной впереди резца (совпадает с положением режущей кромки инструмента – точка А). Для температуры θА получена следующая формула:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.