Значения постоянных коэффициентов и жесткости jст входящих в формулу (293), приведены в табл. 32.
Таблица 32.
Значение величин входящих в формулу (293).
|
Марка сплава |
Cpy |
Ypy |
Xpy |
mPy |
NPy |
kPy |
jст |
|
Ал 2 Ал 9 Д 16 Т АМЦ-50 МА 2-1 Мл 5 |
16,7 16,75 15,35 22,25 18,50 5,25 |
0,82 0,82 0,74 0,70 0,40 0,40 |
1,0 1,0 1,0 1,0 0,7 0,7 |
1,0 1,0 1,0 1,0 1,0 1,0 |
-1,0 -1,0 -1,26 -1,45 -1,4 1,0 |
1,0 1,0 1,0 1,0 1,0 1,0 |
1200 1160 1500 1300 1400 1500 |
На основании выполненных теоретических расчетов [35] получена формула для момента инерции поперечного сечения концевых фрез
JФ=4,5*10-4*DФ4*z2.5 м4. (294)
Значения подачи sz, вычисленные по формуле (293), не могут превышать значений подачи на зуб, определяемых на основе ограничений, накладываемых требованиями к шероховатости обработанной поверхности.
Формула (293) не учитывает жесткости обрабатываемой детали, так как ввиду конструктивной сложности обрабатываемых на фрезерных станках деталей теоретически определить их жесткость сравнительно сложно. При обработке нежестких деталей целесообразно с помощью специальных приспособлений определять возможные деформации обрабатываемых деталей под действием сил резания и учитывать эти деформации программой обработки. Для расчета оптимальных режимов резания при точении и фрезеровании на станках с ЧПУ по приведенным выше методике и формулам была составлена программа для ЭВМ «Минск-22М», по которой электронно-вычислительная машина выдает значение оптимальной скорости резания, число оборотов шпинделя и значение минутной подачи с учетом требований точности обработки и шероховатости обработанной поверхности.
Применение режимов резания по приведенной методике позволило повысить производительность в среднем на 15% при обработке деталей из цветных сплавов на станках с числовым программным управлением.
ПРИМЕНЕНИЕ МЕТОДА ПОДОБИЯ ПРИ ЭКСПЕРИМЕНТАЛЬНЫХ ИССЛЕДОВАНИЯХ КАЧЕСТВА ПОВЕРХНОСТНОГО СЛОЯ
Для получения обобщенных и достоверных зависимостей параметров качества поверхностного слоя от различных технологических факторов может быть успешно использован метод подобия [4, 44], причем конкретное его применение при изучении остаточных напряжений, глубины наклепа и шероховатости поверхности состоит в следующем.
Остаточные напряжения. Теоретически показано (см. гл. II и работу [44]), что в общем случае суммарные остаточные напряжения являются функцией большого количества технологических факторов, которые могут быть объединены
Pe=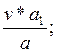 F=
F=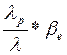 ; D=
; D=![]()
E= ![]() ;
G=
;
G=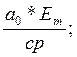 P=
P=![]()
U=cos α; K=![]() ; и L=
; и L=![]() ;
;
следующими критериями подобия:
где a0—
коэффициент линейного расширения обрабатываемого материала, 1/°С; R—радиус обрабатываемой поверхности, м; y≥a — переменная
координата, направленная по радиусу вглубь детали (начало координат смещено на
величину а вверх от поверхности; на поверхности ![]()
В общем случае на основе экспериментов должна находиться функция вида
![]() =f(Pe,F,D,E,G,P,U,K,L). (295)
=f(Pe,F,D,E,G,P,U,K,L). (295)
В степенном виде зависимость имеет выражение
![]() =
=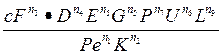 (296)
(296)
где c,n1,n2,n3…,n9— некоторые постоянные величины.
При экспериментальном определении суммарных остаточных напряжений в поверхностном слое при точении конкретной детали с заданной глубиной резания t резцом с известными геометрическими параметрами и свойствами инструментального материала критерии подобия F,G,P,U и Lмогут не учитываться как имеющие постоянные значения. В этом случае выражение принимает вид
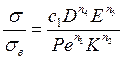 (297)
(297)
где σв— введен вместо σs
Если рассматривать процессы резания, выполняемые при постоянной подаче s острозаточенным резцом (p1=const), то критерии D и Е принимают постоянные значения, а формула для остаточных напряжений имеет более простой вид:
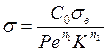 (298)
(298)
где C0,n1 и n2— постоянные величины, определяемые путем обработки экспериментальных зависимостей .
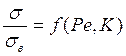
Например, при обработке стали 13Х11Н2В2МФ резцами из сплава ВК6М была получена следующая формула для определения остаточных напряжений (t=1*10-3 м, s=0.23*10-3 м);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.