Представляет значительный интерес теоретическое определение значений оптимальной температуры резания по максимуму отношения контактных твердостей инструментального и обрабатываемого материалов [23], [41], когда они рассматриваются функцией температуры (рис. 31). В отдельных случаях оптимальная температура резания может определяться по провалу
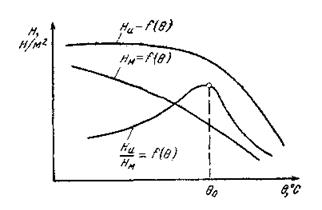 |
Рис. 31 Теоретическое определение оптимальной температуры резания
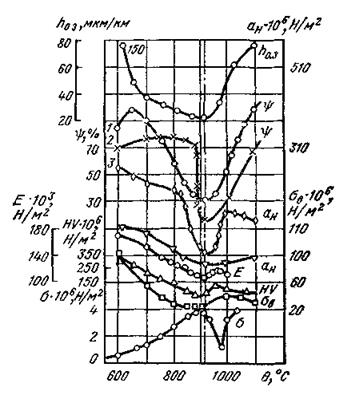 |
Рис. 32 Влияние температуры на механические свойства технического железа и интенсивность износа резца из сплава Т15К6 при точении деталей из стали Э [24]:
1 - деформируемое железо, 2 - литое железо; (99,99%); σв - прочность; HV - твёрдость;
Ем - модуль нормальной упругости; ψ – относительное сужение; ан – ударная вязкость стали Э пластичности (минимуму относительного сужения или относительного удлинения образца), когда ее изменение также рассматривается в зависимости от температуры (рис. 32).
Для определения оптимальной температуры резания А. И. Белоусовым [5] предложена приближенная формула
![]() где
где 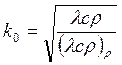 при
при ![]() и
и
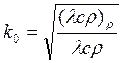 при
при ![]() (199)
(199)
![]() —
произведение коэффициента теплопроводности
—
произведение коэффициента теплопроводности ![]() и
удельной объемной теплоемкости
и
удельной объемной теплоемкости ![]() обрабатываемого
материала;
обрабатываемого
материала; ![]() — то же для резца;
— то же для резца; ![]() —температура
термостойкости инструментального материала, °С.
—температура
термостойкости инструментального материала, °С.
Для определения ![]() получена
также формула (258).
получена
также формула (258).
УРАВНЕНИЕ ОБРАБАТЫВАЕМОСТИ ДЛЯ ОПТИМАЛЬНОГО РЕЗАНИЯ
Установлено, что
оптимальному резанию соответствуют оптимальная температура ![]() и минимальное или минимально-стабилизированное
значение силы резания Pzmin Подставляя значения
и минимальное или минимально-стабилизированное
значение силы резания Pzmin Подставляя значения ![]() и Pzmin в уравнение (198), получим уравнение обрабатываемости
для оптимального резания в виде
и Pzmin в уравнение (198), получим уравнение обрабатываемости
для оптимального резания в виде
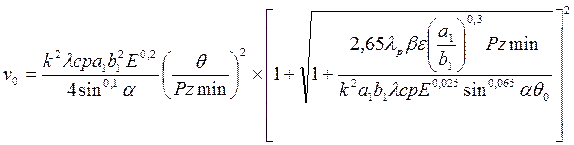 (200)
(200)
Для определения минимально-стабилизированного значения силы Pzmin получена следующая теоретическая формула [41]:
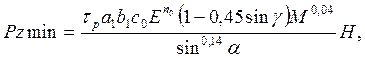 (201)
(201)
где с0 = 3,65; n0=0,125 при Е<=0,05;
с0=5,31; n0==0,25 при 0,05<=Е<=0,1;
с0=7,60; n0=0,40 при E>=0,l;
M = b/b1
; b — суммарная
длина рабочих частей режущих кромок, М; E-p1/a1 ![]() Н/м2; а1 и b1 м; γ и α- передний и задний углы.
Н/м2; а1 и b1 м; γ и α- передний и задний углы.
Формула (201) содержит в себе только величины, известные до опыта, и поэтому позволяет определять Pzmin без проведения экспериментов.
Подставив выражение (201) в уравнение (200), получим формулу для оптимальной скорости резания в окончательном виде:
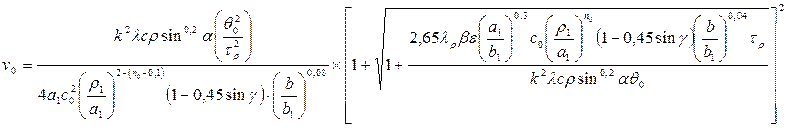 (202)
(202)
Формула (202) является основным уравнением обрабатываемости сталей и сплавов. Она содержит в себе все величины, известные до опыта, и поэтому позволяет прогнозировать оптимальные скорости резания до постановки опытов»
Если принять во внимание, что величины а1 , b1 и b являются функциями глубины резания t, подачи s, геометрических параметров λ, φ, φ1 и r, а оптимальная температура θ0 функцией свойств обрабатываемого и инструментального материалов, то формула (202) учитывает влияние на скорость резания v0 более 20 различных факторов.
Числовой пример. Требуется сравнить обрабатываемость (уровни скоростей резания) нескольких различных сталей и сплавов при следующих постоянных данных: k=3,4; t=2-10-3 м; s=0,2-10-3 м; γ=10°; α=100; φ=45°; φ1=45°; r=l-10-3 м; p1=0,01*10-3 м; β=1,22 рад; ε=1,57 рад.
При этик данных формула оптимальной скорости принимает вид
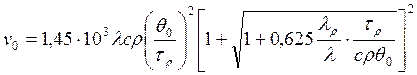 (203)
(203)
Формула (203) показывает, что при рассмотрении конкретной пары резец — деталь обрабатываемость определяется значением оптимальной температуры, а также физико-механическими свойствами обрабатываемого и инструментального материалов.
Таблица 8
Оптимальные скорости резания сталей и сплавов
|
Обрабатываемый материал |
|
|
|
|
|
|
|
Сталь 45 13Х12НВМФА ВТ5-1 ХН62МВКЮ Сплав с прогнозируемыми свойствами |
40,2 26,6 12,8 17,3 10 |
5 4,25 2,7 4,7 4 |
202 113,5 34,4 81,6 40 |
450 725 600 1470 2000 |
950 1045 940 950 1000 |
5,35 1,415 0,60 0,235 0,0835 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.