Теоретическое определение параметров процесса резания ширина и толщина среза при несвободном резании. Теоретический метод определения обрабатываемости материалов резанием, страница 25

где θ_И—температура плавления инструментального материала, 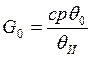равная температуре плавления кобальта 1490° С;  и  — соответственно оптимальная скорость резания и толщина среза при подаче s = l*10^-3 м; δ — относительное удлине-ние образца из обрабатываемого материала при растяжении. Выбор наиболее эффективного инструментального материала производится на основе сравнения нескольких режущих материалов при резании одного и того же рассматриваемого материала при постоянной геометрии инструмента и неизменных значениях глубины резания и подачи. Формула (202) для оптимальной скорости может быть записана в следующей более простой форме:

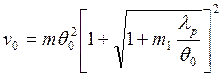 (213)

где m и m₁ — постоянные величины, определяемые выражениями

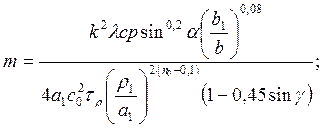
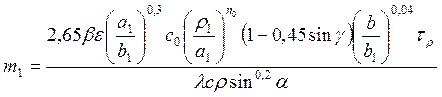
Рекомендуется  следующий  порядок  расчета  коэффициента износостойкости инструментальных материалов:

1)  постоянные величины m и m₁ определяются по принятым значениям глубины резания, подачи, геометрии инструмента, а также свойствам обрабатываемого материала;

2)  оптимальные температуры резания θ₀ заданного обрабатываемого материала определяются описанными выше методами для всей группы сравниваемых инструментальных материалов, включая и эталонный и значения λ_pдля температур θ₀/2;

3)  значения v₀,  v₀', h₀ и h_0Э определяются по формулам (213) и (211) соответственно для всех инструментальных материалов;

4)  коэффициенты износостойкости    k_T рассчитываются    по формуле (210), и по его максимальному значению определяется наиболее рациональный инструментальный материал.

Эффективный инструментальный материал можно определять также по экономическому критерию С_э (формула получена Ю. Е. Кононовым):

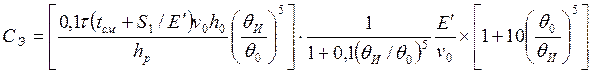 (214)

где τ—безразмерная величина, равная 0,95; t_см — время смены затупившегося инструмента, с; S₁ —затраты, связанные с эксплуатацией режущего инструмента за период его стойкости, коп; Е' — сумма затрат, связанная с эксплуатацией станка в течение одной секунды его работы, коп/с; h_р — критерий затупления инструмента, м.

Величина С_э рассчитывается для всей группы инструментальных материалов. Наиболее эффективным инструментальным материалом считается тот, которому будет соответствовать минимальное значение С_э. Рассмотренные методы определения эффективного инструментального материала по износостойкости и экономическому критерию не учитывают его динамической прочности.

ОПРЕДЕЛЕНИЕ РАЦИОНАЛЬНОЙ ГЕОМЕТРИИ ИНСТРУМЕНТА ПО ИЗНОСОСТОЙКОСТИ

Выбор рациональной геометрии инструмента является важным этапом проектирования операций механической обработки. Эта задача возникает, когда для обработки рассматриваемой стали или сплава уже выбран наиболее рациональный инструментальный материал, т. е. когда свойства обрабатываемого и инструментального материалов известны (являются постоянными значения  λ, cρ, a, τ_p, λ_p, θ₀ и т. д.). На данном этапе развития науки о резании материалов задача определения рациональной геометрии инструмента может быть приближенно решена применительно к условиям оптимального резания, когда за основу принимаются уравнения для оптимальной скорости резания (202), оптимального относительного износа (211) и положение о том, что наиболее рациональная геометрия инструмента при прочих равных условиях должна обеспечивать наиболее высокое значение коэффициента износостойкости k_T. Если наряду со свойствами обрабатываемого и инструментального материалов при сравнении геометрических параметров инструмента считать постоянными t, s, p₁ и r, то уравнение обрабатываемости (202) может быть представлено в следующем виде

при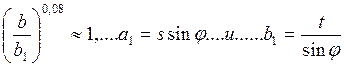

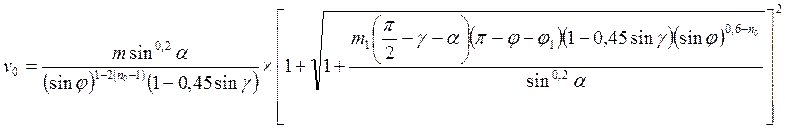(215)

где m и m₁ — постоянные величины, определяемые выражениями

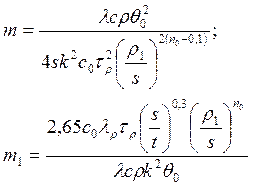
Формула (215) позволяет изменять углы резца α, γ, φ, и φ₁. При постоянных значениях m и m₁ необходимо найти сочетание этих четырех углов, обеспечивающее максимальное значение v₀, минимальное значение h₀ и максимальное значение k_T при необходимой прочности инструмента и шероховатости поверхности. Так как уравнение (215) содержит четыре искомых угла инструмента, то при решении задачи необходимо задаваться наиболее реальными значениями трех углов, например α, γ, φ₁, и находить соответствующий им главный угол в плане φ