Определять рациональную геометрию инструмента необходимо в следующем порядке:
1)определить расчетные значения постоянных величин: λ, cρ, τp, λp, θ0, ρ1 ,r, t, s;
2)определить толщину среза a1 и ширину среза b1, с0,, n0, критерии F, Е, D, приняв в качестве эталонных наиболее распространенные значения углов резца
(γ=10°, α=10°, φ=45,φ1 = 15°);
3) определить предварительное значение Ре по формуле при k = 3,5:
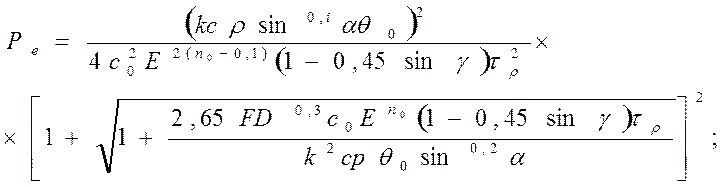 (216)
(216)
4) Найти для Ре по табл. 7 уточненное значение коэффициента k;
5) определить значения постоянных величин m и m1;
6) по формуле (215) найти наибольшее значение υ0 путем использования различных сочетаний углов α, γ, φ и φ1 при удовлетворении требований получения необходимой прочности инструмента и шероховатости поверхности;
7)по формулам (210) и (211) определить минимальное значение h0 и максимальное значение kт.
РАСЧЕТ РАДИАЛЬНОГО ИЗНОСА, РАДИАЛЬНОЙ СТОЙКОСТИ ИНСТРУМЕНТА И ПРОИЗВОДИТЕЛЬНОСТИ
Характеристикой размерной стойкости инструмента может служить поверхностный относительный износ [23, 24]. При рассмотрении лишь зоны нормального износа имеем
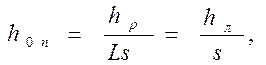 (217)
(217)
где hp – конечная величина радиального износа, мкм;
L=vTP – общая длина пути резания за период размерной стойкости TP сек, м.
Из формулы (217) для размерного износа Получим
![]() (218)
(218)
Подставляя в выражения (217) и (218)
уравнение скорости резания (197), получим следующие формулы, устанавливающие
связь износа и стойкости инструмента с основными параметрами процесса резания для конечной величины
радиального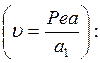 износа
износа
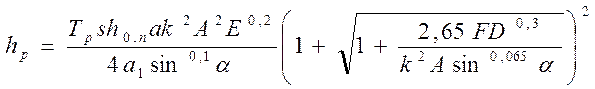 (219)
(219)
для скорости радиального износа инструментов
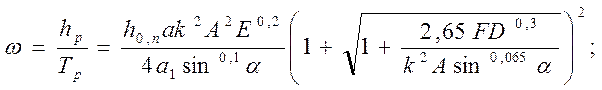 (220)
(220)
для относительного поверхностного износа
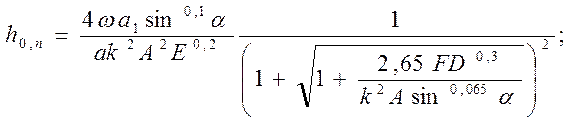 (221)
(221)
для размерной стойкости инструментов
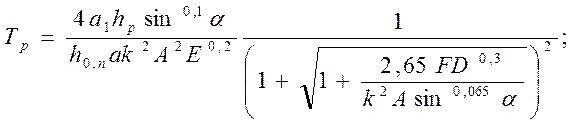 (222)
(222)
В формулы (219) — (222) входят известные уже критерий A, F, D и E. При назначении режимов резания задаются обычно допустимо величиной износа hp, исходя из требуемой шероховатости обрабатываемой 'поверхности и точности обработки, и определенной стойкостью инструмента Tp, Следовательно, скорость износа ω можно считать величиной известной, и тогда, как следует из формулы (221), ho.п при выбранной геометрии инструмента, известных свойствах обрабатываемого и инструментального материалов и принятых t и s становится функцией лишь критерия А, т. е. отношения Pz/θ, зависящего от уровня применяемых скоростей резания. Увеличение v в широких пределах всегда вызывает возрастание температуры резания θ, хотя темп ее роста неодинаков для различных интервалов изменения υ. Сила резания Pz, наоборот, три увеличении υ в широком диапазоне изменяется немонотонно. Следовательно, отношение Pz/θ и относительный поверхностный износ ho.п также изменяются немонотонно. При определенной скорости резания
υ0 сила резания принимает минимальное или минимально-стабилизированное значение Pzmin. Относительный поверхностный износ также становится минимальным, а температура резания принимает оптимальное значение. Оптимальным значениям υ0 и θ0 соответствуют оптимальные значения параметров процесса резания, характеризующих износ и стойкость инструмента. Для оптимального резания получены следующие формулы:
для оптимального (наименьшего) относительного поверхностного износа
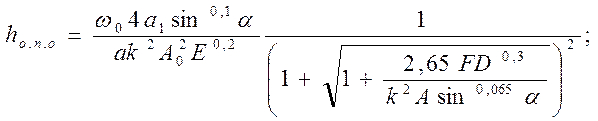 (223)
(223)
для оптимальной интенсивности размерного износа
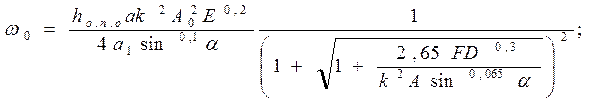 (224)
(224)
 |
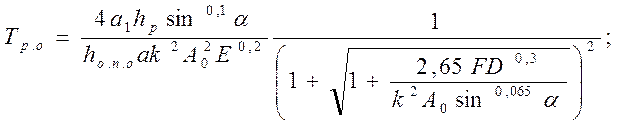 (225)
(225)
для площади поверхности (М2), обработанной за период максимальной размерной стойкости,
![]() (226)
(226)
для числа деталей (шт.), которое можно обработать за период максимальной размерной стойкости,
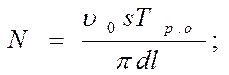 (227)
(227)
где d и l – соответственно диаметр и длина обрабатываемой поверхности, м.
В формулах (223) - (225) критерий A0 определяется выражением
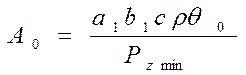 (228)
(228)
ВЗАИМОСВЯЗЬ РАДИАЛЬНОГО ИЗНОСА С ИЗНОСОМ ПО ЗАДНЕЙ ПОВЕРХНОСТИ ИНСТРУМЕНТА
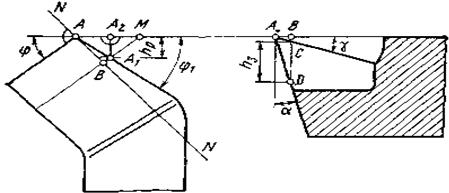
Целесообразно установить теоретическую связь радиального износа инструментов hp с износом по задней поверхности hз (рис. 39). При получении радиального износа hp и износа по задней поверхности вершина резца из положения А переходит в положение A1. Величина АВ связана с износом по задней поверхности следующим образом:
![]()
![]()
Следовательно:
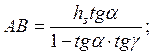
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.