Теоретическое определение параметров процесса резания ширина и толщина среза при несвободном резании. Теоретический метод определения обрабатываемости материалов резанием, страница 30

Для плоских деталей(дисков) расчет температурных остаточных напряжений проводился как с учетом охлаждения с наведением упругих деформаций, так и при возникновении пластических деформаций при охлаждении. В случае охлаждения с наведением упругих деформаций остаточные температурные напряжения определяютсяпо формулам:     при 0yy_ои

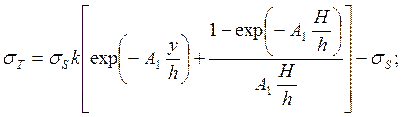                                  (244)

при y>y_ои

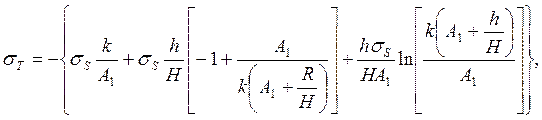(245)

где; 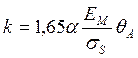 ;  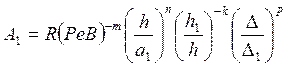—безразмерный комплекс; H/h — отношение толщины пластины(диска) H к глубине пластических деформаций h; a_s — предел текучести обрабатываемого материала; у_ои — граница раздел упругих и пластических деформаций при нагреве диска;      

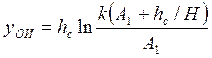
В случае охлаждения с наведением пластических деформаций в металле температурные остаточные напряжения определяются по формулам:                                                                        при 0yy_oo

σ_T = σ_S     (246)

при y_ooyy_oи

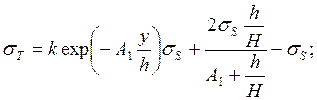(247) при  y>y_ои

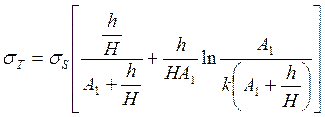 (248)

где у₀₀ — граница раздела упругих и пластических деформаций при охлаждении диска. Для определения величины у₀₀ получена формула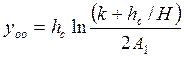

Остаточные напряжения от действия силового фактора  (от действия нагрузки без учета влияния температуры). Силы, действующие на передней и задней поверхностях инструмента, взаимосвязаны между собой, но для определения напряженного поля они рассматривались как отдельные группы сил. Полагалось, что протяженность упругопластической среды, ограниченной поверхностью ABD (см. рис. 41) и простирающейся неограниченно вниз, велика в направлении, перпендикулярном к плоскости чертежа (плоская деформация).

На основании использования теоремы о разгрузке Генки, известных положений из теории упругости и пластичности, данных других исследователей [18], а также применения методов теории подобия получены следующие уравнения для расчета остаточных напряжений от силового фактора;

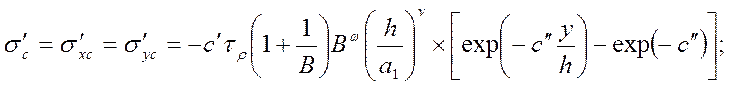(249)

 (250)

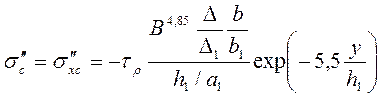                                (251)

где b — суммарная длина режущих кромок инструмента; b₁ — ширина среза. Числовые значения величин  определяют по табл. 14.

Остаточные напряжения от структурных и фазовых превращений. При механической обработке процессы фазовых и микроструктурных превращений приводят к возникновению остаточных напряжений. Рассмотрим вопрос о расчете тангенциальных остаточных напряжений. Цилиндрическую деталь радиусом R₁ подвергали нагреву на поверхности до температуры θ и воздействию тангенциальной составляющей силы резания P_z, которые вызвали структурные превращения в ее поверхностных слоях. Допустим, что первоначальная структура детали была по всему объему одинаковой и имела плотность γ₁ .

Таблица 14

Значения величин  и  для определения остаточных напряжений oт силового фактора

Под действием температурного и деформационного влияния слой детали толщиной d=R₁—r подвергся по всему объему равномерным фазовым или микроструктурным превращениям и в результате (после полного остывания) принял новую структуру с плотностью γ₂ Пусть γ₂>γ₁ тогда удельный объем v₂<v₁

Следовательно, после остывания радиус R₁ уменьшится до R₂ а величина d до d₁. Заметим, что при γ₂<γ₁  наоборот, d увеличится до d₁ на величину (d₁—d). Уменьшение радиуса R₁ до R₂ вызовет остаточные деформации. Определим относительные остаточные деформации по радиусу из условия равенства масс плоских колец толщиной d и d₁ при одинаковой их длине: