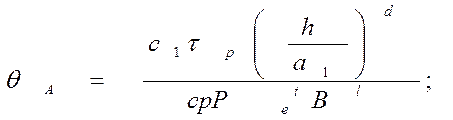Теоретическое определение параметров процесса резания ширина и толщина среза при несвободном резании. Теоретический метод определения обрабатываемости материалов резанием, страница 29

(240)

тде c₁, d, t и l – постоянные величины, значения которых даны в табл. 11.

Таблица   11

Значения постоянных величин c₁d, t и l для определения

С помощью ЭЦВМ были произведены –параметры относительной суммарной температуры θ/θ_А  в поверхностном слое детали по уравнению (239), результаты которые представлены на рис. 41. Качественный анализ получением) температурного слоя I позволяет сделать следующие основные выводы:

1)  температурное поле как на поверхности, так и по мере удаления вглубь от поверхности детали носит экстремальный характер;

2)  координата, соответствующая максимуму температуры на задней контактной поверхности, расположёна, примерно Вт середине контактной площадки инструмента с Деталью;

3)  по мере удаления  вглубь от поверхности значения  относительных температур убывают,  а  координата,  соответствующая максимуму относительной температуры, сдвигается вправо, что объясняется превышением скорости движения источника тепла над скоростью распространения тепла твердом теле.

Наибольший интерес с точки зрения определения теоретическим методом остаточных напряжений представляет максимальное значение температуры в поверхностям слое детали. На основе расчетов на ЭЦВМ и построения Графических зависимостей максимальной относительной температуры θ_m/θ_А  от отдельных безразмерных    параметров    получено    упрощенное уравнение в виде экспоненциальной зависимости

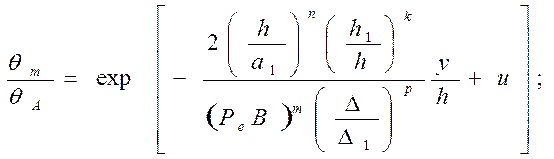 (241)

где R, n, k, m, p, и u – постоянные численные величины, значения которых даны в табл. 12.ч

Следует отметить, что при обработке особенно труднообрабатываемых материалов (жаропрочные стали и сплавы, титановые сплавы, закаленные стали и др.) диапазон рациональных режимов резания соответствует  Р_еВ<30, и поэтому наибольший практический интерес представляет формула

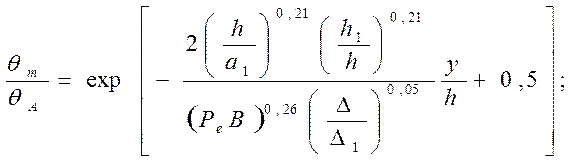 (242)

Сравнительными расчетами установлено, что погрешность, формул (241) и (242) по отношению к исходному уравнению. (239) не превышает 3-5%.

Температурные остаточные напряжения. При выводе теоретических зависимостей остаточных напряжений от технологических факторов были приняты следующие допущения:

Значения величин R, n, r, m, p, u для определения θ_m.  Таблица 12

материал детали принят идеально упругопластическим;

рассматривалась двухмерная деформационная система (плоская деформация);

остаточные напряжения определялись на основании теоремы о разгрузке.

Вывод уравнений для температурных остаточных напряжений осуществлен [44] на основе использования метода Абрамова, научных результатов других исследователей и приведенных выше формул (240) и (241). ,

Для цилиндрических деталей уравнение для определения тангенциальных и осевых температурных остаточных напряжений .имеет вид

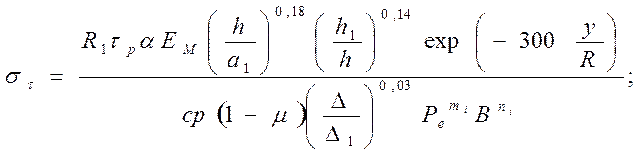(243)

где R₁, m₁ и n₁ – постоянные величины, значения которых даны в табл. R – радиус обработанной поверхности детали; α и μ коэффициенты линейного расширения и Пуассона материала детали.

Таблица   13

Значения R₁,m_1,n₁ для определения